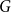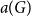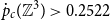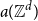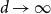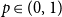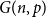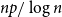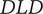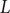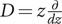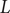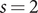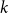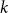Refine search
Actions for selected content:
52379 results in Statistics and Probability
On the joint survival probability of two collaborating firms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 August 2023, pp. 369-384
- Print publication:
- June 2024
-
- Article
- Export citation
On the exponential growth rates of lattice animals and interfaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 912-955
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A diagnostic model based on routine blood examination for serious bacterial infections in neonates–a cross-sectional study
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 31 July 2023, e137
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting empirical spectral distribution for the non-backtracking matrix of an Erdős-Rényi random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 956-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase transition for the generalized two-community stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 385-400
- Print publication:
- June 2024
-
- Article
- Export citation
Legionellosis on the rise: A scoping review of sporadic, community-acquired incidence in the United States
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 28 July 2023, e133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On L-derivatives and biextensions of Calabi–Yau motives
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 28 July 2023, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A hybrid data mining framework for variable annuity portfolio valuation
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 July 2023, pp. 580-595
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Seroprevalence of Toxoplasma gondii and associated risk factors for infection in the Netherlands: third cross-sectional national study
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 28 July 2023, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Inverse Problems and Data Assimilation
-
- Published online:
- 27 July 2023
- Print publication:
- 10 August 2023
Disparity-persistence and the multistep friendship paradox
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 290-298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviors of aggregated Markov processes
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 299-317
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COVID-19 second wave and clinical characteristics of cases in Uganda: A retrospective cross-sectional survey of confirmed SARS-CoV-2 cases, March–June 2021
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 July 2023, e142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A general model for how attributes can reduce polarization in social groups
-
- Journal:
- Network Science / Volume 11 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 July 2023, pp. 536-559
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the maximum number of edges in
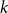 $k$-critical graphs
$k$-critical graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 24 July 2023, pp. 900-911
-
- Article
- Export citation
Continuous latent position models for instantaneous interactions
-
- Journal:
- Network Science / Volume 11 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 July 2023, pp. 560-588
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Attitudes toward COVID-19 vaccination of healthcare workers in Israel and vaccination rates during vaccine rollout
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A switching Gaussian process latent force model for the identification of mechanical systems with a discontinuous nonlinearity
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterization of the optimal average cost in Markov decision chains driven by a risk-seeking controller
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 July 2023, pp. 340-367
- Print publication:
- March 2024
-
- Article
- Export citation
Impact of implementing a free varicella vaccination policy on incidence in Wuxi City, China: an interrupted time series analysis
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 20 July 2023, e125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation