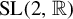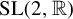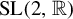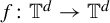Contents
Original Article
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium measures for two-sided shift spaces via dimension theory
- Part of:
-
- Published online by Cambridge University Press:
- 10 September 2024, pp. 427-466
-
- Article
- Export citation
Hereditarily frequently hypercyclic operators and disjoint frequent hypercyclicity
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2025, pp. 3021-3072
-
- Article
- Export citation
On possible limit functions on a Fatou component in non-autonomous iteration
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2024, pp. 719-806
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A trichotomy for hitting times and escape rates for a class of unimodal maps
- Part of:
-
- Published online by Cambridge University Press:
- 11 August 2025, pp. 3663-3697
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of:
-
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniformity aspects of
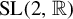 ${\mathrm {SL}}(2,{\mathbb R})$ cocycles and applications to Schrödinger operators defined over Boshernitzan subshifts
${\mathrm {SL}}(2,{\mathbb R})$ cocycles and applications to Schrödinger operators defined over Boshernitzan subshifts
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1734-1756
-
- Article
- Export citation
Transcendental Julia sets of minimal Hausdorff dimension
- Part of:
-
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
-
- Article
- Export citation
Symbolic dynamics for Hénon maps near the boundary of the horseshoe locus
-
- Published online by Cambridge University Press:
- 23 May 2024, pp. 140-174
-
- Article
- Export citation
Decidability of the isomorphism problem between multidimensional substitutive subshifts
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2054-2094
-
- Article
- Export citation
Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2025, pp. 2695-2723
-
- Article
- Export citation
Homomorphisms from aperiodic subshifts to subshifts with the finite extension property
-
- Published online by Cambridge University Press:
- 28 April 2025, pp. 3073-3089
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic data rigidity of Anosov automorphisms with Jordan blocks
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2024, pp. 1129-1160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On non-tameness of the Ellis semigroup
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2025, pp. 3419-3429
-
- Article
- Export citation
Rigidity of Lyapunov exponents for derived from Anosov diffeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1444-1460
-
- Article
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1757-1776
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth orbit equivalence rigidity for dissipative geodesic flows
- Part of:
-
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3698-3727
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for equilibrium states on amenable group subshifts
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2025, pp. 2414-2438
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformational rigidity of integrable metrics on the torus
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2024, pp. 467-503
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subshifts of finite symbolic rank
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2024, pp. 807-848
-
- Article
-
- You have access
- Open access
- HTML
- Export citation