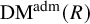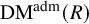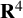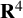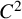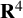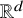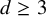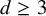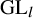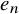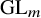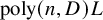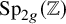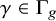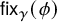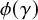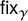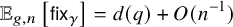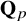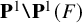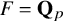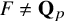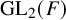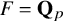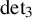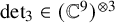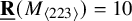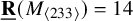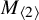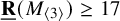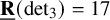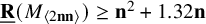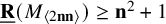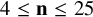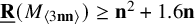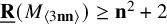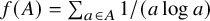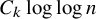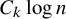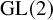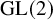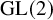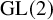Contents
Algebraic and Complex Geometry
Syntomic complexes and p-adic étale Tate twists
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2023, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Prismatic Dieudonné Theory
- Part of:
-
- Published online by Cambridge University Press:
- 06 January 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Geometry and Geometric Analysis
Stable anisotropic minimal hypersurfaces in
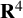 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Sharp smoothing properties of averages over curves
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
A Shuffle Theorem for Paths Under Any Line
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Proof of the Extended Delta Conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
A Proof of the Extended Delta Conjecture – Corrigendum
-
- Published online by Cambridge University Press:
- 06 March 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Shuffle Theorem for Paths Under Any Line – Corrigendum
-
- Published online by Cambridge University Press:
- 06 March 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
The existence of the Kähler–Ricci soliton degeneration
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the relative minimal model program for fourfolds in positive and mixed characteristic
-
- Published online by Cambridge University Press:
- 24 March 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics
Homoclinic orbits, multiplier spectrum and rigidity theorems in complex dynamics
-
- Published online by Cambridge University Press:
- 08 May 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational Mathematics
Rigid continuation paths II. structured polynomial systems
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
On the Torelli Lie algebra
-
- Published online by Cambridge University Press:
- 14 April 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Comparison of quantizations of symmetric spaces: cyclotomic Knizhnik–Zamolodchikov equations and Letzter–Kolb coideals
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
The Asymptotic Statistics of Random Covering Surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Factorisation de la cohomologie étale p-adique de la tour de Drinfeld
- Part of:
-
- Published online by Cambridge University Press:
- 26 May 2023, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theoretical Computer Science
New lower bounds for matrix multiplication and
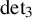 $\operatorname {det}_3$
$\operatorname {det}_3$
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
A proof of the Erdős primitive set conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Resolution of the Erdős–Sauer problem on regular subgraphs
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2023, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Exotic Monoidal Structures and Abstractly Automorphic Representations for
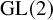 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$
- Part of:
-
- Published online by Cambridge University Press:
- 03 August 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation