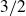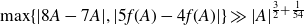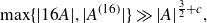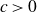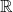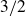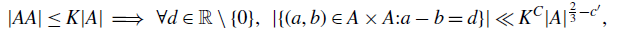Refine listing
Actions for selected content:
1417150 results in Open Access
Passive bionic motion of a flexible film in the wake of a circular cylinder: chaos and periodicity, flow–structure interactions and energy evolution
-
- Journal:
- Journal of Fluid Mechanics / Volume 986 / 10 May 2024
- Published online by Cambridge University Press:
- 10 May 2024, A29
-
- Article
- Export citation
A new morphotype description of Arbacia spatuligera Valenciennes, 1846 (Arbacioida, Echinoidea) and bathymetric range extension from mesophotic reefs of the central coast of Chile
-
- Journal:
- Journal of the Marine Biological Association of the United Kingdom / Volume 104 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e48
-
- Article
- Export citation
ANZ VOLUME 65 ISSUE 4 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 10 May 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Economic resilience and the dynamics of capital stock
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 10 May 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On conformally flat minimal Legendrian submanifolds in the unit sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-30
-
- Article
- Export citation
Ian Bradley, Breathers of an Ampler Day: Victorian Views of Heaven (Durham, Sacristy Press, 2023) vii + 195 Pbk £14.99 ISBN 978-1-78959-291-7
-
- Journal:
- Journal of Anglican Studies / Volume 23 / Issue 1 / May 2025
- Published online by Cambridge University Press:
- 10 May 2024, pp. 263-264
-
- Article
- Export citation
The actuarial sources of the rise in unfunded liabilities in America's defined benefit plans in the 21st century
-
- Journal:
- Journal of Pension Economics & Finance / Volume 24 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 10 May 2024, pp. 235-255
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Terror Trials: Life and Law in Delhi’s Courts. By Mayur R. Suresh. New York: Fordham University Press, 2023, 255 pp. $32.00 paperback
-
- Journal:
- Law & Society Review / Volume 58 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 341-343
- Print publication:
- June 2024
-
- Article
- Export citation
First record of the phyllosoma larva of the pygmy locust lobster Scyllarus pygmaeus (Crustacea, Decapoda) in the eastern Mediterranean sea
-
- Journal:
- Journal of the Marine Biological Association of the United Kingdom / Volume 104 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e49
-
- Article
- Export citation
High-gain TM11 mode equilateral triangular patch antenna with shorting pins and triangular short horn
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 16 / Issue 6 / July 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1009-1023
-
- Article
- Export citation
On Harnack inequality and harmonic Schwarz lemma
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 940-954
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANZ VOLUME 65 ISSUE 4 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 10 May 2024, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Small-scale turbulent characteristics in transcritical wall-bounded flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 986 / 10 May 2024
- Published online by Cambridge University Press:
- 10 May 2024, A36
-
- Article
- Export citation
A better than
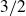 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 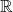 $\mathbb R$
$\mathbb R$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 11-22
- Print publication:
- July 2024
-
- Article
- Export citation
How Autocrats Abuse Power: Resistance to Trump and Trumpism. By Richard L. Abel. Abingdon and New York: Routledge, 2024. Paperback, ISBN 978-1-032-62881-3
-
- Journal:
- Law & Society Review / Volume 58 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 350-352
- Print publication:
- June 2024
-
- Article
- Export citation
Drawings of Roman Mosaics in the Topham Collection, Eton College Library. By P. Witts. BAR international series 3064. BAR Publishing, Oxford, 2021. Pp. xvi + 193, illus. Price £48. isbn 9781407358987 (pbk); 9781407358994 (PDF eBook). - Spectacle and Display: A Modern History of Britain's Roman Mosaic Pavements. By M. Dawson. Archaeopress Roman archaeology 79. Archaeopress, Oxford, 2021. Pp. vi + 246, illus. Price £40. isbn 9781789698312 (pbk); 9781789698329 (PDF eBook).
-
- Article
- Export citation
Zonal jets and eddy tilts in barotropic geostrophic turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 986 / 10 May 2024
- Published online by Cambridge University Press:
- 10 May 2024, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Catenaries and minimal surfaces of revolution in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation