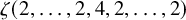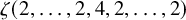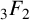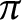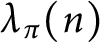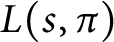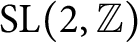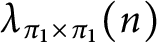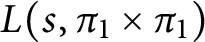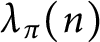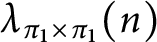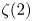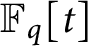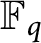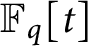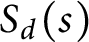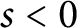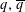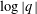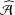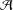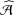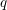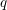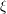Refine search
Actions for selected content:
26 results
Symmetric multiple zeta functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zagier–Hoffman’s Conjectures in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 October 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaluation of
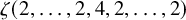 $ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
$ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation
Mean value of real Dirichlet characters using a double Dirichlet series
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 22 March 2023, pp. 1135-1151
- Print publication:
- December 2023
-
- Article
- Export citation
Generating function of multiple polylog of Hurwitz type
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 1-17
- Print publication:
- February 2024
-
- Article
- Export citation
OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 215-226
- Print publication:
- April 2023
-
- Article
- Export citation
Cancellation of two classes of dirichlet coefficients over Beatty sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 234-252
- Print publication:
- March 2022
-
- Article
- Export citation
ON A WEIGHTED SUM OF MULTIPLE $\mathbf{{T}}$
 -VALUES OF FIXED WEIGHT AND DEPTH
-VALUES OF FIXED WEIGHT AND DEPTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 398-405
- Print publication:
- December 2021
-
- Article
- Export citation
Depth-graded motivic multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 529-572
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of multizeta values over
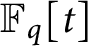 $\mathbb {F}_q[t]$ at negative integers
$\mathbb {F}_q[t]$ at negative integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 9-29
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
A CLASS OF NONHOLOMORPHIC MODULAR FORMS II: EQUIVARIANT ITERATED EISENSTEIN INTEGRALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e31
-
- Article
-
- You have access
- Open access
- Export citation
DERIVATION RELATION FOR FINITE MULTIPLE ZETA VALUES IN
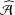 $\widehat{{\mathcal{A}}}$
$\widehat{{\mathcal{A}}}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 260-265
- Print publication:
- April 2021
-
- Article
- Export citation
ON A GENERALISATION OF A RESTRICTED SUM FORMULA FOR MULTIPLE ZETA VALUES AND FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 23-34
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
ANALOGUES OF THE AOKI–OHNO AND LE–MURAKAMI RELATIONS FOR FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 34-40
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Cyclotomic analogues of finite multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2701-2721
- Print publication:
- December 2018
-
- Article
- Export citation
INTERPOLATED SCHUR MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 25 October 2017, pp. 289-307
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
MULTI-POLY-BERNOULLI NUMBERS AND RELATED ZETA FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 19-54
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE DOUBLE SHUFFLE RELATIONS FOR MULTIPLE EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 180-212
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
ZETA ELEMENTS IN DEPTH 3 AND THE FUNDAMENTAL LIE ALGEBRA OF THE INFINITESIMAL TATE CURVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 05 January 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation