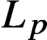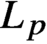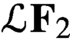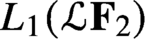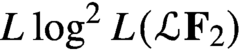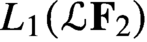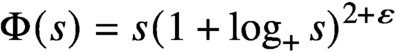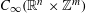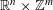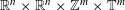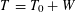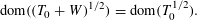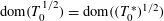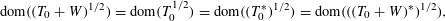Refine search
Actions for selected content:
11 results
Complete positivity order and relative entropy decay
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 February 2025, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Overcoming the timescale barrier in molecular dynamics: Transfer operators, variational principles and machine learning
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 517-673
-
- Article
-
- You have access
- Open access
- Export citation
Matrix calculations for moments of Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 126-150
- Print publication:
- March 2023
-
- Article
- Export citation
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
Regularity theory of Kolmogorov operator revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 24 August 2020, pp. 725-736
- Print publication:
- December 2021
-
- Article
- Export citation
Intertwined Markov processes: the extended Chapman–Kolmogorov equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 123-131
- Print publication:
- February 2018
-
- Article
- Export citation
SOME FELLER SEMIGROUPS ON
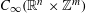 $C_{\infty }(\mathbb{R}^{n}\times \mathbb{Z}^{m})$ GENERATED BY PSEUDO-DIFFERENTIAL OPERATORS
$C_{\infty }(\mathbb{R}^{n}\times \mathbb{Z}^{m})$ GENERATED BY PSEUDO-DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 15 April 2015, pp. 402-413
- Print publication:
- May 2015
-
- Article
- Export citation
ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 12 March 2015, pp. 111-182
- Print publication:
- 2016
-
- Article
- Export citation
Markov Processes with Restart
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 960-968
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Hitting Times, Occupation Times, Trivariate Laws and the Forward Kolmogorov Equation for a One-Dimensional Diffusion with Memory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 860-875
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Convergence of Brownian motion with a scaled Dirac delta potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 403-427
-
- Article
-
- You have access
- Export citation