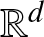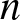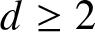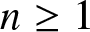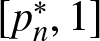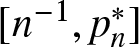Refine search
Actions for selected content:
48569 results in Computer Science
Chapter 11 - Explore and explain: statistics for network data
- from Part II - Applications, tools, and tasks
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 137-164
-
- Chapter
- Export citation
11 - The Fourier Series
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 458-507
-
- Chapter
- Export citation
Chapter 14 - Summarizing and comparing networks
- from Part II - Applications, tools, and tasks
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 223-234
-
- Chapter
- Export citation
12 - The DFT and the FFT
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 508-555
-
- Chapter
- Export citation
Chapter 26 - Embedding and machine learning
- from Part III - Fundamentals
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 429-446
-
- Chapter
- Export citation
Chapter 17 - Research record-keeping
- from Interlude — Good practices for scientific computing
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 283-288
-
- Chapter
- Export citation
Part II - Applications, tools, and tasks
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 63-64
-
- Chapter
- Export citation

The Largest Suslin Axiom
-
- Published online:
- 07 June 2024
- Print publication:
- 27 June 2024

Working with Network Data
- A Data Science Perspective
-
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024
Design issues concerning circular economy assessment methods at the product level: a comparative analysis through a case study of a mobile tiny house
- Part of
-
- Journal:
- Design Science / Volume 10 / 2024
- Published online by Cambridge University Press:
- 05 June 2024, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
‘To Explore the World of Sound’: Music, silence and nation-building in Bing Bang Boom (1969)
-
- Journal:
- Organised Sound / Volume 29 / Issue 2 / August 2024
- Published online by Cambridge University Press:
- 05 June 2024, pp. 111-130
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Modern Robotics
- Mechanics, Planning, and Control
-
- Published online:
- 04 June 2024
- Print publication:
- 25 May 2017
Colourising the past: Digital visual repatriation of colourised Sámi photography
- Part of
-
- Journal:
- Memory, Mind & Media / Volume 3 / 2024
- Published online by Cambridge University Press:
- 04 June 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Usefulness of Information for Achieving Goals with Disjunctive Premises
-
- Journal:
- The Knowledge Engineering Review / Volume 39 / 2024
- Published online by Cambridge University Press:
- 04 June 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the probability of a Pareto record
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 752-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Advancing digital healthcare engineering for aging ships and offshore structures: an in-depth review and feasibility analysis
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 03 June 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal experiment design with adjoint-accelerated Bayesian inference
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 31 May 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A linear linear lambda-calculus
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 10 / November 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1103-1137
-
- Article
- Export citation
FINITARY UPPER LOGICISM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1172-1247
- Print publication:
- December 2024
-
- Article
- Export citation