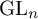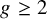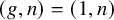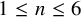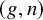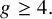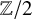Refine listing
Actions for selected content:
380 results in 14Fxx
PRISMATIC COHOMOLOGY OF RIGID ANALYTIC SPACES OVER DE RHAM PERIOD RING
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 January 2026, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Čech cohomology of infinite projective spaces, flag manifolds, and related spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGY OF THE BASIC UNRAMIFIED PEL UNITARY RAPOPORT-ZINK SPACE OF SIGNATURE
 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomology of the Bruhat–Tits strata in the supersingular locus of the
 $\mathrm {GU}(1,n-1)$ Shimura variety at a ramified prime
$\mathrm {GU}(1,n-1)$ Shimura variety at a ramified prime
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXCEPTIONAL PAIRS ON DEL PEZZO SURFACES AND SPACES OF COMPATIBLE FEIGIN-ODESSKII BRACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 25 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 October 2025, pp. 339-373
- Print publication:
- January 2026
-
- Article
- Export citation
On proper splinters in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 December 2025, pp. 2493-2544
- Print publication:
- October 2025
-
- Article
- Export citation
Hodge theory of abelian covers of algebraic varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 September 2025, e159
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AVERAGING FUNCTORS IN FARGUES’ PROGRAM FOR
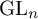 $\mathrm {GL}_n$
$\mathrm {GL}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 25 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 24 September 2025, pp. 45-84
- Print publication:
- January 2026
-
- Article
- Export citation
On the Nori and Hodge realisations of Voevodsky motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 13 October 2025, pp. 2155-2201
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundedness of the p-primary torsion of the Brauer group of products of varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 August 2025, e134
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The higher direct images of locally constant group schemes from the Kummer log flat topology to the classical flat topology
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 04 August 2025, pp. 667-693
- Print publication:
- November 2025
-
- Article
- Export citation
RIGID INNER FORMS OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2181-2256
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of Brauer groups of moduli stacks of stable curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Brauer groups of moduli of genus three curves, abelian threefolds and plane curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1664-1697
- Print publication:
- July 2025
-
- Article
- Export citation
COHERENCE OF MULTIPLIER SUBMODULE SHEAVES ON GENERIC COMPLEX TORI
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 666-673
-
- Article
- Export citation
Revisiting Dwork cohomology: visibility and divisibility of Frobenius eigenvalues in rigid cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1215-1249
- Print publication:
- June 2025
-
- Article
- Export citation
Inversion of Adjunction for the minimal exponent
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free summands of stably free modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 May 2025, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation