Refine listing
Actions for selected content:
134 results in 16Exx
The rank of a hypergeometric system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 August 2010, pp. 284-318
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Bimodules and branes in deformation quantization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 11 August 2010, pp. 105-160
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
On semi-infinite cohomology of finite-dimensional graded algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 23 February 2010, pp. 480-496
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Simplicial cohomology of augmentation ideals in l1(G)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 97-109
-
- Article
-
- You have access
- Export citation
Linear Koszul duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 16 December 2009, pp. 233-258
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
GORENSTEIN PROJECTIVE, INJECTIVE AND FLAT MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 395-407
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Cluster structures for 2-Calabi–Yau categories and unipotent groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 1035-1079
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
On graded centres and block cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 489-514
-
- Article
-
- You have access
- Export citation
Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky versus Hanamura
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 39-97
- Print publication:
- January 2009
-
- Article
- Export citation
ON A DUALITY THEOREM OF WAKAMATSU
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 343-350
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
HOCHSCHILD (CO)HOMOLOGY OF ℤ2×ℤ2-GALOIS COVERINGS OF QUANTUM EXTERIOR ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 35-54
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Baer and quasi-Baer properties of group rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 285-296
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Cotorsion modules and relative pure-injectivity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-244
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Finite Generation of the Extension Algebra Ext
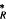 (M, M)
(M, M)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-374
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
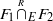 , and the corresponding derived intersection
, and the corresponding derived intersection 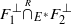 . We also propose applications to Hecke algebras.
. We also propose applications to Hecke algebras. (and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM
(and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM (
(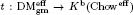 ;
; 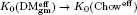 . A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if
. A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if 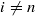 (where
(where 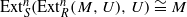 and
and 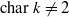 , and let Λ
, and let Λ (M, M)
(M, M)
