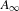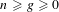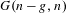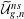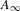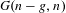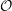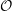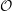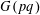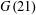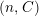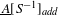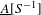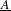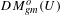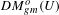Refine listing
Actions for selected content:
134 results in 16Exx
Rational Cup Product and Algebraic K0-Groups of Rings of Continuous Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 607-622
-
- Article
- Export citation
Integrable Derivations and Stable Equivalences of Morita Type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 343-362
-
- Article
- Export citation
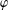 $\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND
$\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND 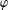 $\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
$\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 January 2018, pp. 274-278
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
TILTING CHAINS OF NEGATIVE CURVES ON RATIONAL SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 20 December 2017, pp. 26-41
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
MODULI OF CURVES WITH NONSPECIAL DIVISORS AND RELATIVE MODULI OF
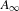 $A_{\infty }$-STRUCTURES
$A_{\infty }$-STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 30 October 2017, pp. 1295-1329
- Print publication:
- November 2019
-
- Article
- Export citation
KOSZUL CALCULUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 18 October 2017, pp. 361-399
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
On categories
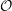 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 2445-2481
- Print publication:
- December 2017
-
- Article
- Export citation
A CATEGORIFICATION OF A QUANTUM FROBENIUS MAP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 20 July 2017, pp. 899-939
- Print publication:
- September 2019
-
- Article
- Export citation
Cluster categories for marked surfaces: punctured case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 15 June 2017, pp. 1779-1819
- Print publication:
- September 2017
-
- Article
- Export citation
Homomorphisms between standard modules over finite-type KLR algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 621-646
- Print publication:
- March 2017
-
- Article
- Export citation
UNIT-REGULAR MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 23 February 2017, pp. 1-15
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
AN EXPLICIT DIAGONAL RESOLUTION FOR A NON-ABELIAN METACYCLIC GROUP
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 March 2017, pp. 499-517
- Print publication:
- 2017
-
- Article
- Export citation
CANONICAL AND
 $n$ -CANONICAL MODULES OF A NOETHERIAN ALGEBRA
$n$ -CANONICAL MODULES OF A NOETHERIAN ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 20 October 2016, pp. 165-203
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
A RECOLLEMENT APPROACH TO GEIGLE–LENZING WEIGHTED PROJECTIVE VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 71-105
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
EXT-FINITE MODULES FOR WEAKLY SYMMETRIC ALGEBRAS WITH RADICAL CUBE ZERO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 108-121
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
COHOMOLOGICAL LENGTH FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 136-161
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
Homogeneity of cohomology classes associated with Koszul matrix factorizations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 2071-2112
- Print publication:
- October 2016
-
- Article
- Export citation
HOMOLOGICAL DIMENSIONS OF CROSSED PRODUCTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 401-420
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
NON-COMMUTATIVE LOCALIZATIONS OF ADDITIVE CATEGORIES AND WEIGHT STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 4 / September 2018
- Published online by Cambridge University Press:
- 24 May 2016, pp. 785-821
- Print publication:
- September 2018
-
- Article
- Export citation
REGULARITY CRITERION AND CLASSIFICATION FOR ALGEBRAS OF JORDAN TYPE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 69-95
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation