Refine listing
Actions for selected content:
134 results in 16Exx
FINITISTIC DIMENSIONS AND PIECEWISE HEREDITARY PROPERTY OF SKEW GROUP ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 509-517
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Frobenius categories, Gorenstein algebras and rational surface singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 502-534
- Print publication:
- March 2015
-
- Article
- Export citation
HOMOGENEOUS PBW DEFORMATION FOR ARTIN–SCHELTER REGULAR ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 53-68
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Matrix factorizations via Koszul duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1549-1578
- Print publication:
- September 2014
-
- Article
- Export citation
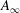 $A_{\infty }$-algebras associated with curves and rational functions on
$A_{\infty }$-algebras associated with curves and rational functions on 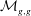 $\mathcal{M}_{g,g}$. I
$\mathcal{M}_{g,g}$. I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 621-667
- Print publication:
- April 2014
-
- Article
- Export citation
Pro-
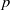 $\lowercase p$ Iwahori–Hecke algebras are Gorenstein
$\lowercase p$ Iwahori–Hecke algebras are Gorenstein
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 28 November 2013, pp. 753-809
- Print publication:
- October 2014
-
- Article
- Export citation
USING IDEALS TO PROVIDE A UNIFIED APPROACH TO UNIQUELY CLEAN RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 258-274
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON CLEAN LAURENT SERIES RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 421-427
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON A QUESTION OF HARTWIG AND LUH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 271-278
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
QUASI MULTIPLICATION AND
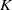 $K$-GROUPS
$K$-GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 257-267
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
TRIVIAL MAXIMAL 1-ORTHOGONAL SUBCATEGORIES FOR AUSLANDER 1-GORENSTEIN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 133-144
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
THE TOP LEFT DERIVED FUNCTORS OF THE GENERALISED
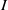 $I$-ADIC COMPLETION
$I$-ADIC COMPLETION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 04 January 2013, pp. 259-266
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Hochschild homology of Hopf algebras and free Yetter–Drinfeld resolutions of the counit
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 17 December 2012, pp. 658-678
- Print publication:
- April 2013
-
- Article
- Export citation
On inverse categories and transfer in cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 187-210
-
- Article
-
- You have access
- Export citation
Tensor structure on kC-mod and cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 349-370
-
- Article
-
- You have access
- Export citation
FP-INJECTIVE COMPLEXES AND FP-INJECTIVE DIMENSION OF COMPLEXES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 25 August 2011, pp. 163-187
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Algèbres simpliciales S1-équivariantes, théorie de de Rham et théorèmes HKR multiplicatifs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1979-2000
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
ON REGULAR MODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 280-287
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
On the centre of a triangulated category
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 07 April 2011, pp. 443-466
-
- Article
-
- You have access
- Export citation
On two examples by Iyama and Yoshino
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 591-612
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
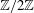
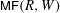
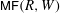
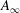
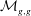
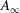
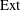
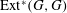
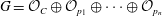
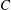
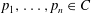
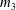
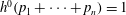
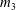
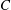
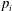
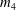
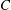
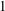
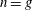
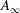
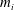
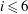
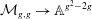
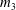
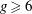
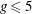
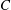
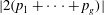
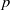
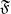
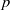
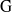
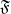
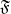
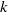
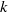

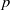
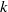
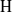
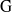
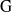
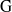
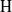
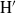
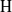
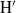
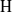
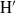
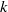
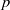
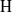
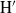
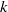
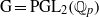
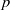
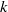
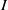
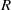
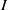
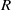
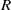
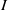
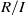
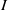
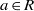
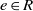
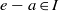
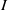
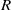
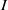
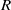
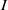
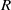
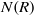
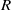
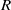
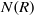
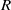
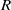
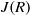
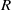
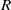
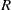
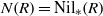
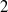
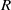
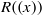
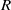
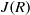
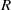
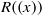
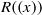
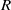
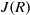

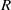
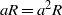
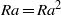

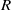
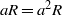
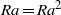
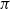
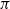
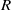
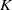
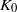
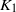
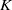
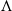
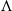
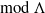
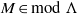
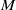
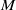
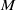
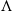
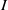
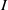
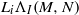
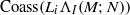
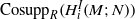
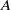
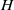
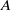
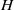
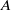
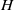
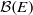
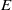
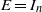
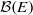
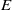
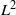
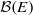
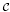 , being a Mackey functor on
, being a Mackey functor on 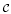 be a finite category and let
be a finite category and let 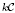 and show that
and show that 