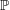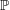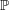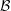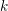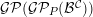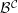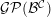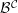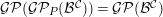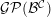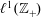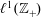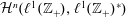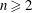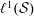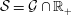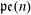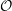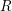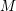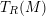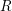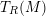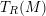Refine listing
Actions for selected content:
134 results in 16Exx
FLAT RING EPIMORPHISMS OF COUNTABLE TYPE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 383-439
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Formality of
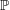 $\mathbb{P}$-objects
$\mathbb{P}$-objects
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 973-994
- Print publication:
- May 2019
-
- Article
- Export citation
Formality conjecture for K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 23 April 2019, pp. 902-911
- Print publication:
- May 2019
-
- Article
- Export citation
n-T-COTORSION-FREE MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 297-311
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
EPSILON-STRONGLY GROUPOID-GRADED RINGS, THE PICARD INVERSE CATEGORY AND COHOMOLOGY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 233-259
- Print publication:
- January 2020
-
- Article
-
- You have access
- Open access
- Export citation
A Representation Theoretic Study of Non-Commutative Symmetric Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 875-887
-
- Article
- Export citation
Gerstenhaber Bracket on the Hochschild Cohomology via An Arbitrary Resolution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 06 February 2019, pp. 817-836
-
- Article
- Export citation
On triangle equivalences of stable categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 955-974
- Print publication:
- April 2020
-
- Article
- Export citation
Universal localizations via silting
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 511-532
- Print publication:
- April 2019
-
- Article
- Export citation
GORENSTEIN PROJECTIVE OBJECTS IN FUNCTOR CATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 1-41
- Print publication:
- December 2020
-
- Article
- Export citation
Simplicial (Co)-homology of
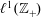 $\ell ^{1}(\mathbb{Z}_{+})$
$\ell ^{1}(\mathbb{Z}_{+})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 756-766
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Factorizations in Bounded Hereditary Noetherian Prime Rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 395-442
-
- Article
- Export citation
The Primitive Spectrum and Category
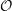 ${\mathcal{O}}$ for the Periplectic Lie Superalgebra
${\mathcal{O}}$ for the Periplectic Lie Superalgebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 625-655
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
AC-GORENSTEIN RINGS AND THEIR STABLE MODULE CATEGORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 181-198
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
The Gorenstein-projective modules over a monomial algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 02 October 2018, pp. 1115-1134
- Print publication:
- December 2018
-
- Article
- Export citation
COARSE COHERENCE OF METRIC SPACES AND GROUPS AND ITS PERMANENCEPROPERTIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 12 September 2018, pp. 422-433
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
The Projective Leavitt Complex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1155-1177
-
- Article
- Export citation
Characterizations and Direct Sums of Unit-Endoregular Modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 10 August 2018, pp. 1103-1112
-
- Article
- Export citation
A NOTE ON ENTROPY OF AUTO-EQUIVALENCES: LOWER BOUND AND THE CASE OF ORBIFOLD PROJECTIVE LINES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 26 June 2018, pp. 86-103
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
GORENSTEIN HOMOLOGICAL PROPERTIES OF TENSOR RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 188-208
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation