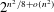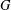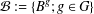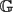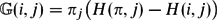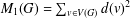Refine listing
Actions for selected content:
1073 results in 05Cxx
Convergence of Achlioptas Processes via Differential Equations with Unique Solutions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 14 October 2015, pp. 154-171
-
- Article
- Export citation
THE TYPICAL STRUCTURE OF MAXIMAL TRIANGLE-FREE GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 09 October 2015, e20
-
- Article
-
- You have access
- Open access
- Export citation
Distinct Distances from Three Points
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 30 September 2015, pp. 623-632
-
- Article
- Export citation
The Random Graph Intuition for the Tournament Game
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 23 September 2015, pp. 76-88
-
- Article
- Export citation
FINITE SYMMETRIC GRAPHS WITH 2-ARC-TRANSITIVE QUOTIENTS: AFFINE CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 17 September 2015, pp. 13-18
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Distance between two random k-out digraphs, with and without preferential attachment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 858-879
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A FORMULA FOR THE NUMBER OF SPANNING TREES IN CIRCULANT GRAPHS WITH NONFIXED GENERATORS AND DISCRETE TORI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 25 August 2015, pp. 365-373
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Simple Containers for Simple Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 17 August 2015, pp. 448-459
-
- Article
- Export citation
ON ISOMORPHISMS OF VERTEX-TRANSITIVE CUBIC GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 13 August 2015, pp. 341-349
-
- Article
-
- You have access
- Export citation
Universality of Graphs with Few Triangles and Anti-Triangles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 29 July 2015, pp. 560-576
-
- Article
- Export citation
An Improvement of the Beck–Fiala Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 06 July 2015, pp. 380-398
-
- Article
- Export citation
On the “Preconditioning” Function Used in Planewave DFT Calculations and its Generalization
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 167-179
- Print publication:
- July 2015
-
- Article
- Export citation
A Hitting Time Formula for the Discrete Green's Function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 29 June 2015, pp. 362-379
-
- Article
- Export citation
The Interpolation Method for Random Graphs with Prescribed Degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 19 June 2015, pp. 436-447
-
- Article
- Export citation
Topological realizations and fundamental groups of higher-rank graphs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 143-168
-
- Article
-
- You have access
- Export citation
SOME RESULTS ON THE DIFFERENCE OF THE ZAGREB INDICES OF A GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 177-186
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Asymptotic Properties of a Random Graph with Duplications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 375-390
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
First Passage Percolation on Inhomogeneous Random Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 589-610
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
First Passage Percolation on Random Geometric Graphs and an Application to Shortest-Path Trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 328-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Phase Transitions for Random Geometric Preferential Attachment Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 565-588
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation