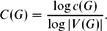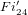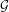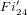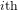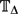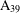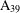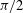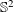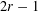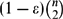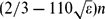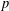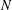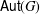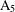Refine listing
Actions for selected content:
1073 results in 05Cxx
On the Normalized Shannon Capacity of a Union
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 766-767
-
- Article
- Export citation
Structure of the
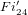 $Fi_{24}^{\prime }$ maximal
$Fi_{24}^{\prime }$ maximal  $2$ -local geometry point-line collinearity graph
$2$ -local geometry point-line collinearity graph
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 105-154
-
- Article
-
- You have access
- Export citation
SELECTED TOPICS IN SPECTRAL GRAPH THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 511-512
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON ARC-REGULAR FROBENIUS METACIRCULANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 20-29
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Coexistence in Preferential Attachment Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 09 February 2016, pp. 797-822
-
- Article
- Export citation
Inapproximability of the Partition Function for the Antiferromagnetic Ising and Hard-Core Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 500-559
-
- Article
- Export citation
CAYLEY GRAPHS OVER A FINITE CHAIN RING AND GCD-GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 353-363
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
A 2-ARC TRANSITIVE PENTAVALENT CAYLEY GRAPH OF
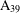 $\text{A}_{39}$
$\text{A}_{39}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 441-446
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ORTHOGONAL COLORINGS OF THE SPHERE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 04 February 2016, pp. 492-501
- Print publication:
- 2016
-
- Article
- Export citation
UPPER BOUND THEOREM FOR ODD-DIMENSIONAL FLAG TRIANGULATIONS OF MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 909-928
- Print publication:
- 2016
-
- Article
- Export citation
The Multiple-Orientability Thresholds for Random Hypergraphs†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 28 December 2015, pp. 870-908
-
- Article
- Export citation
Manipulative Waiters with Probabilistic Intuition
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 823-849
-
- Article
- Export citation
Local Maxima of Quadratic Boolean Functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 633-640
-
- Article
- Export citation
Path Ramsey Number for Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 612-622
-
- Article
- Export citation
Contagions in random networks with overlapping communities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 973-988
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The extinction time of a subcritical branching process related to the SIR epidemic on a random graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1195-1201
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
-
- Article
-
- You have access
- Export citation
AUTOMORPHISM GROUPS OF SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 238-247
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Perfect Packings in Quasirandom Hypergraphs II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 27 October 2015, pp. 595-611
-
- Article
- Export citation
TRANSFERENCE FOR THE ERDŐS–KO–RADO THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 26 October 2015, e23
-
- Article
-
- You have access
- Open access
- Export citation