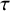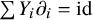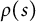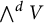Refine listing
Actions for selected content:
231 results in 05Exx
Wreath Macdonald operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutation graph of support
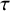 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-one dual characters of flagged Weyl modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-23
-
- Article
- Export citation
Orthogonal roots, Macdonald representations, and quasiparabolic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schubert polynomial expansions revisited
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 July 2025, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration on complex Grassmannians, deformed monotone Hurwitz numbers, and interlacing phenomena
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Supersolvability of built lattices and Koszulness of generalized Chow rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1284-1312
- Print publication:
- June 2025
-
- Article
- Export citation
Gelfand–Tsetlin crystals
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 May 2025, pp. 1-14
-
- Article
- Export citation
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shuffle formula in science fiction for Macdonald polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1075-1127
- Print publication:
- May 2025
-
- Article
- Export citation
Newton–Maclaurin type inequalities for linear combinations of elementary symmetric functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-18
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetric multiple zeta functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On exterior powers of reflection representations, II
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-23
-
- Article
- Export citation
AUTOMORPHISM GROUPS OF BICOSET DIGRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 30-46
- Print publication:
- August 2025
-
- Article
- Export citation
The asymptotics of the expected Betti numbers of preferential attachment clique complexes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 940-968
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A raising operator formula for Macdonald polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pebble trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinite flags and Schubert polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation