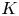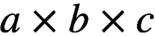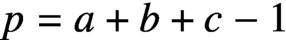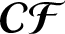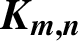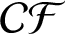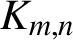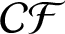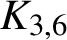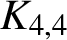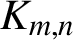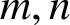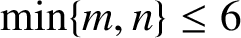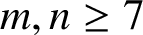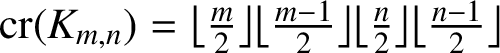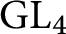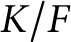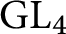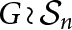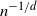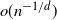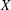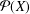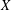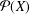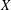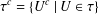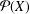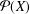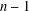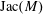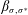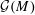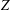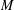Refine listing
Actions for selected content:
231 results in 05Exx
POWERS OF BINOMIAL EDGE IDEALS WITH QUADRATIC GRÖBNER BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 31 March 2021, pp. 233-255
- Print publication:
- June 2022
-
- Article
- Export citation
On symmetric intersecting families of vectors
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 18 March 2021, pp. 899-904
-
- Article
- Export citation
One-relator groups and algebras related to polyhedral products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 15 January 2021, pp. 128-147
- Print publication:
- February 2022
-
- Article
- Export citation
FACTORIZATION LENGTH DISTRIBUTION FOR AFFINE SEMIGROUPS III: MODULAR EQUIDISTRIBUTION FOR NUMERICAL SEMIGROUPS WITH ARBITRARILY MANY GENERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 12 January 2021, pp. 21-35
- Print publication:
- August 2022
-
- Article
- Export citation
Dynamics of plane partitions: Proof of the Cameron–Fon-Der-Flaass conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 07 December 2020, 62
-
- Article
-
- You have access
- Open access
- Export citation
ON PROBLEMS OF
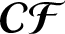 $\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR
$\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR 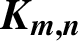 $\boldsymbol{K}_{\boldsymbol{m,n}}$
$\boldsymbol{K}_{\boldsymbol{m,n}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 203-210
- Print publication:
- October 2021
-
- Article
- Export citation
A proof of the linear Arithmetic Fundamental Lemma for
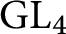 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 381-427
- Print publication:
- April 2022
-
- Article
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
- Print publication:
- June 2021
-
- Article
- Export citation
ON THE DEPTH OF SYMBOLIC POWERS OF EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 28-40
- Print publication:
- March 2022
-
- Article
- Export citation
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
THE COMBINATORICS OF TENSOR PRODUCTS OF HIGHER AUSLANDER ALGEBRAS OF TYPE A
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 526-546
- Print publication:
- September 2021
-
- Article
- Export citation
HALF-SPACE MACDONALD PROCESSES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
Gelfand Pairs Involving the Wreath Product of Finite Abelian Groups with Symmetric Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 91-97
- Print publication:
- March 2021
-
- Article
- Export citation
Factorization problems in complex reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 899-946
- Print publication:
- August 2021
-
- Article
- Export citation
FRIEZE PATTERNS WITH COEFFICIENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 March 2020, e17
-
- Article
-
- You have access
- Open access
- Export citation
Tropical friezes and the index in higher homological algebra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 23-49
- Print publication:
- July 2021
-
- Article
- Export citation
Limit theorems for process-level Betti numbers for sparse and critical regimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 1-31
- Print publication:
- March 2020
-
- Article
- Export citation
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
On Extensions for Gentle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 249-292
- Print publication:
- February 2021
-
- Article
- Export citation
GEOMETRIC BIJECTIONS FOR REGULAR MATROIDS, ZONOTOPES, AND EHRHART THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 December 2019, e45
-
- Article
-
- You have access
- Open access
- Export citation