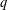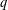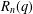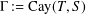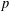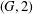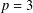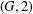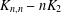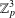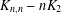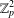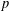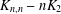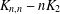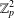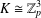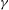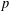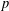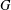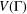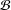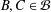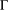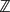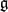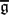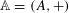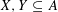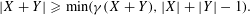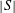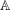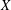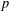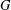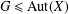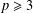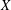Refine listing
Actions for selected content:
231 results in 05Exx
THE ANNIHILATOR OF TENSOR SPACE IN THE
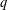 $q$ -ROOK MONOID ALGEBRA
$q$ -ROOK MONOID ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 77-86
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
DISTRIBUTIVE LATTICES OF TILTING MODULES AND SUPPORT τ-TILTING MODULES OVER PATH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 503-511
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 07 June 2016, pp. 165-166
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
FINITE NORMAL 2-GEODESIC TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 338-348
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
2-ARC-TRANSITIVE REGULAR COVERS OF
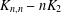 $K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP
$K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP 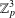 $\mathbb{Z}_{p}^{3}$
$\mathbb{Z}_{p}^{3}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 145-170
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
LOWER BOUND THEOREMS AND A GENERALIZED LOWER BOUND CONJECTURE FOR BALANCED SIMPLICIAL COMPLEXES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 441-477
- Print publication:
- 2016
-
- Article
- Export citation
UPPER BOUND THEOREM FOR ODD-DIMENSIONAL FLAG TRIANGULATIONS OF MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 909-928
- Print publication:
- 2016
-
- Article
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
FINITE SYMMETRIC GRAPHS WITH 2-ARC-TRANSITIVE QUOTIENTS: AFFINE CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 17 September 2015, pp. 13-18
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
DUAL EQUIVALENCE GRAPHS I: A NEW PARADIGM FOR SCHUR POSITIVITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 22 July 2015, e12
-
- Article
-
- You have access
- Open access
- Export citation
EXPLICIT CONSTRUCTION OF COMPANION BASES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 357-384
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
JACK–LAURENT SYMMETRIC FUNCTIONS FOR SPECIAL VALUES OF PARAMETERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 599-616
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
ISOMORPHIC INDUCED MODULES AND DYNKIN DIAGRAM AUTOMORPHISMS OF SEMISIMPLE LIE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 187-203
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
STABILITY PATTERNS IN REPRESENTATION THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e11
-
- Article
-
- You have access
- Open access
- Export citation
Generalized friezes and a modified Caldero–Chapoton map depending on a rigid object
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-124
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
- Print publication:
- 2016
-
- Article
- Export citation
ON GRAPHS OF PRIME VALENCY ADMITTING A SOLVABLE ARC-TRANSITIVE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 13 May 2015, pp. 214-227
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
 $\wedge$-TRANSITIVE DIGRAPHS PRESERVING A CARTESIAN DECOMPOSITION
$\wedge$-TRANSITIVE DIGRAPHS PRESERVING A CARTESIAN DECOMPOSITION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 31 March 2015, pp. 85-107
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation