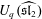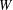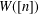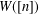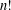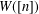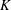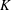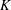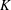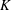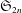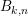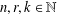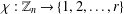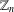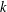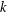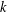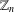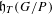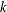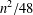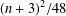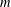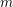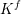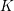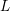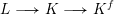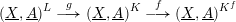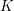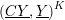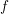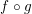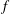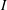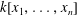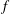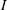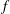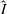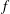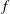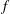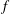Refine listing
Actions for selected content:
231 results in 05Exx
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e39
-
- Article
-
- You have access
- Open access
- Export citation
DEGREE OF THE
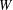 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 186-200
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
THE THICKNESS OF SCHUBERT CELLS AS INCIDENCE STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 145-156
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Polynomials from Combinatorial
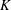 $K$-theory
$K$-theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 29-62
- Print publication:
- February 2021
-
- Article
- Export citation
THE POLYTABLOID BASIS EXPANDS POSITIVELY INTO THE WEB BASIS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 19 August 2019, e26
-
- Article
-
- You have access
- Open access
- Export citation
On Betti numbers of flag complexes with forbidden induced subgraphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 June 2019, pp. 567-600
- Print publication:
- May 2020
-
- Article
- Export citation
CLUSTER CATEGORIES FROM GRASSMANNIANS AND ROOT COMBINATORICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 03 June 2019, pp. 322-354
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
AN IDENTITY OF PARABOLIC KAZHDAN–LUSZTIG POLYNOMIALS ARISING FROM SQUARE-IRREDUCIBLE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 April 2019, pp. 81-93
- Print publication:
- February 2021
-
- Article
- Export citation
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
ORIENTED FLIP GRAPHS, NONCROSSING TREE PARTITIONS, AND REPRESENTATION THEORY OF TILING ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 147-182
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
INTEGER POLYGONS OF GIVEN PERIMETER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 131-147
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Boardman–Vogt tensor products of absolutely free operads
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 367-385
- Print publication:
- February 2020
-
- Article
- Export citation
AN ALGORITHM TO CONSTRUCT THE LE DIAGRAM ASSOCIATED TO A GRASSMANN NECKLACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2019, pp. 85-91
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Flow Polytopes and the Space of Diagonal Harmonics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1495-1521
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
PBW Bases and Marginally Large Tableaux in Types B and C
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 37-54
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Almost Gentle Algebras and their Trivial Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 489-504
-
- Article
- Export citation
The homotopy theory of polyhedral products associated with flag complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 206-228
- Print publication:
- January 2019
-
- Article
- Export citation
Newton Complementary Duals of
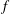 $f$-Ideals
$f$-Ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 231-241
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation