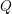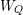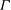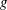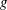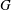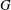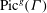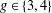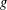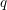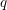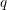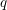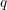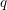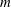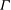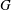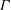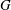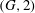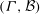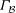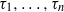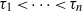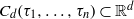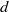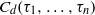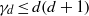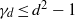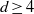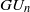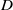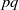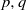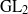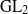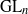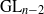Refine listing
Actions for selected content:
231 results in 05Exx
The (7, 4)-Conjecture in Finite Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 10 February 2015, pp. 680-686
-
- Article
- Export citation
ADVENTURES IN INVARIANT THEORY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 105-115
-
- Article
-
- You have access
- Export citation
ROW CONVEX TABLEAUX AND BOTT–SAMELSON VARIETIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 23 October 2014, pp. 315-330
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Quotient closed subcategories of quiver representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 568-602
- Print publication:
- March 2015
-
- Article
- Export citation
ESTIMATION AND COMPUTATION WITH MATRICES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 175-176
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
CANONICAL REPRESENTATIVES FOR DIVISOR CLASSES ON TROPICAL CURVES AND THE MATRIX–TREE THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 26 September 2014, e24
-
- Article
-
- You have access
- Open access
- Export citation
FINITE 3-GEODESIC TRANSITIVE BUT NOT 3-ARC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 183-190
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Spectral theory for the
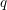 $q$-Boson particle system
$q$-Boson particle system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 1-67
- Print publication:
- January 2015
-
- Article
- Export citation
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
SYMMETRIC GRAPHS WITH 2-ARC TRANSITIVE QUOTIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 275-288
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
FINITE
 $s$-GEODESIC TRANSITIVE GRAPHS
$s$-GEODESIC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 November 2013, pp. 175-176
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
NORMAL CYCLIC POLYTOPES AND CYCLIC POLYTOPES THAT ARE NOT VERY AMPLE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 30 September 2013, pp. 61-77
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Positroid varieties: juggling and geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 19 August 2013, pp. 1710-1752
- Print publication:
- October 2013
-
- Article
- Export citation
Eigenvalues of Hermitian matrices and equivariant cohomology of Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1569-1582
- Print publication:
- September 2013
-
- Article
- Export citation
Topological flatness of local models for ramified unitary groups. II. The even dimensional case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 10 July 2013, pp. 303-393
- Print publication:
- April 2014
-
- Article
- Export citation
Intersecting families in classical Coxeter groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 887-908
-
- Article
-
- You have access
- Export citation
SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS OF ORDER A PRODUCT OF TWO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 322-330
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
TILING BRANCHING MULTIPLICITY SPACES WITH GL
 ${}_{2} $ PATTERN BLOCKS
${}_{2} $ PATTERN BLOCKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 362-374
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
ELUSIVE CODES IN HAMMING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 286-296
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Bases for cluster algebras from surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 07 December 2012, pp. 217-263
- Print publication:
- February 2013
-
- Article
- Export citation