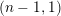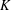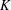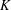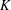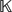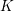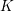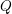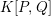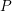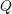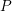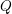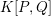Refine listing
Actions for selected content:
231 results in 05Exx
Foundations of Boij–Söderberg theory for Grassmannians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 11 September 2018, pp. 2205-2238
- Print publication:
- October 2018
-
- Article
- Export citation
Line arrangements and configurations of points with an unexpected geometric property
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 2150-2194
- Print publication:
- October 2018
-
- Article
- Export citation
THE LOCAL
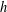 $h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
$h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 258-264
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
CONTINUOUS ASSOCIATION SCHEMES AND HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 July 2018, pp. 361-426
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Chern class formulas for classical-type degeneracy loci
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1746-1774
- Print publication:
- August 2018
-
- Article
- Export citation
A CONJECTURE ON
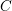 $C$-MATRICES OF CLUSTER ALGEBRAS
$C$-MATRICES OF CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 19 June 2018, pp. 37-46
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
Twisted Brauer monoids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 731-750
- Print publication:
- August 2018
-
- Article
- Export citation
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 27 March 2018, pp. 308-337
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF ACCUMULATION POINTS OF ROOTS FOR TYPE (n - 1, 1) COXETER GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 01 March 2018, pp. 127-157
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
On Zeros of a Polynomial in a Finite Grid
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 310-333
-
- Article
- Export citation
COVERS OF GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 585-601
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
A probabilistic interpretation of the Gaussian binomial coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1295-1298
- Print publication:
- December 2017
-
- Article
- Export citation
INTERPOLATED SCHUR MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 25 October 2017, pp. 289-307
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
DIAGRAM ALGEBRAS, DOMINANCE TRIANGULARITY AND SKEW CELL MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 13-36
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
EQUIVARIANT
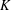 $K$ -THEORY OF GRASSMANNIANS
$K$ -THEORY OF GRASSMANNIANS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 June 2017, e3
-
- Article
-
- You have access
- Open access
- Export citation
THE EXPECTED JAGGEDNESS OF ORDER IDEALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 March 2017, e9
-
- Article
-
- You have access
- Open access
- Export citation
ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 14 March 2017, pp. 705-715
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Equivariant
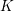 $K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
$K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 09 March 2017, pp. 667-677
- Print publication:
- April 2017
-
- Article
- Export citation
ISOTONIAN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 March 2017, pp. 83-101
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
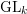
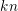
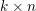
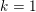
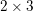
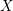
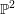
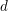
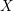
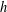
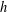
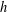
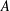
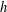
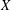
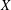
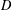
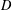
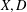
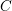
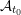
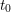
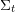
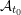
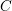

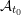
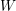
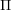
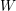

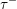
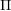
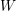
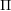
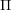
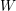
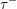
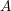
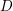
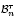 , comparing and contrasting it with the structure of the (untwisted) Brauer monoid
, comparing and contrasting it with the structure of the (untwisted) Brauer monoid 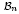 . We characterize Green's relations and pre-orders on
. We characterize Green's relations and pre-orders on