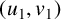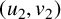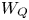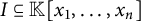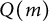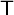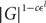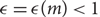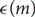Refine listing
Actions for selected content:
231 results in 05Exx
A Laplace transform approach to direct and inverse problems for multi-compartment models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1170-1184
-
- Article
- Export citation
Derived categories of skew-gentle algebras and orbifolds
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 649-674
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE TWO-DISTANCE-TRANSITIVE DIHEDRANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 386-401
- Print publication:
- December 2022
-
- Article
- Export citation
Functorially finite hearts, simple-minded systems in negative cluster categories, and noncrossing partitions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 23 February 2022, pp. 211-243
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariants for metabelian groups of prime power exponent, colorings, and stairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 December 2021, pp. 267-297
- Print publication:
- February 2023
-
- Article
- Export citation
On the multiplication of spherical functions of reductive spherical pairs of type A
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 341-374
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERACTING QUARTER-PLANE LATTICE WALK PROBLEMS: SOLUTIONS AND PROOFS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 339-340
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
Powers of Principal Q-Borel ideals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 633-652
- Print publication:
- September 2022
-
- Article
- Export citation
LIE ALGEBRA MODULES WHICH ARE LOCALLY FINITE AND WITH FINITE MULTIPLICITIES OVER THE SEMISIMPLE PART
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 430-470
- Print publication:
- June 2022
-
- Article
- Export citation
Symmetry of Narayana Numbers and Rowvacuation of Root Posets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL REFLECTION SUBGROUPS OF COMPLEX REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 July 2021, pp. 879-917
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
Bihomogeneous symmetric functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 25 May 2021, pp. 400-408
- Print publication:
- June 2022
-
- Article
- Export citation
Skew characters and cyclic sieving
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 21 May 2021, e41
-
- Article
-
- You have access
- Open access
- Export citation
Involution pipe dreams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 1310-1346
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1324- and 2143-avoiding Kazhdan–Lusztig immanants and k-positivity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 May 2021, pp. 52-82
- Print publication:
- February 2023
-
- Article
- Export citation
Back stable Schubert calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 883-962
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Additive bases via Fourier analysis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 930-941
-
- Article
- Export citation
A Symmetric Function of Increasing Forests
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 April 2021, e35
-
- Article
-
- You have access
- Open access
- Export citation