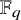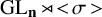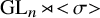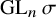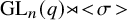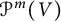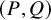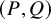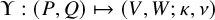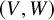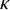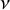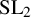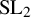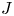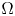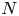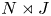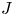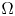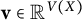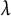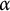Refine listing
Actions for selected content:
231 results in 05Exx
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1664-1685
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pieri rules for skew dual immaculate functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 902-914
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalization of immanants based on partition algebra characters
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1001-1010
- Print publication:
- December 2024
-
- Article
- Export citation
Ideals with componentwise linear powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 833-841
- Print publication:
- September 2024
-
- Article
- Export citation
Delta and Theta Operator Expansions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 March 2024, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorial formulas for shifted dual stable Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 February 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Δ–Springer varieties and Hall–Littlewood polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
E-Polynomials of Generic
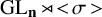 $\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
$\mathbf {\operatorname {\mathrm {GL}}_n\rtimes \!<\!\sigma \!>\!}~$-Character Varieties: Branched Case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COEFFICIENT QUIVERS,
 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 561-617
- Print publication:
- September 2024
-
- Article
- Export citation
Graphical methods and rings of invariants on the symmetric algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2173-2198
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew RSK dynamics: Greene invariants, affine crystals and applications to q-Whittaker polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 October 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EXTERIOR POWERS OF REFLECTION REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 90-102
- Print publication:
- August 2024
-
- Article
- Export citation
A combinatorial model for the transition matrix between the Specht and
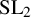 $\operatorname {SL}_2$-web bases
$\operatorname {SL}_2$-web bases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 September 2023, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAYLEY GRAPHS AND GRAPHICAL REGULAR REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 161-162
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Fixed point conditions for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 345-351
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rotor-Routing Induces the Only Consistent Sandpile Torsor Structure on Plane Graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 07 September 2023, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simple eigenvalues of cubic vertex-transitive graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 10 August 2023, pp. 1496-1519
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MacMahon’s statistics on higher-dimensional partitions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation


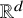
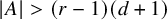

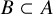
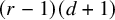
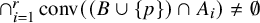
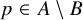
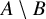
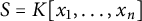
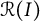
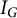
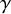
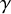
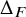
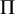
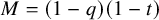
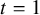
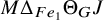
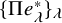
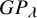
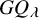
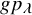
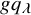
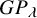
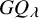
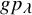
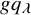
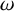
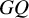
 .
.