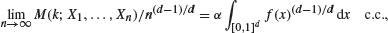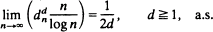Refine listing
Actions for selected content:
1718 results in 05xxx
Addendum to ‘Quasi-renewal estimates’ for modelling DNA replication
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1171-1172
- Print publication:
- December 2000
-
- Article
- Export citation
The formal theory of birth-and-death processes, lattice path combinatorics and continued fractions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 750-778
- Print publication:
- September 2000
-
- Article
- Export citation
Markov paths on the Poisson-Delaunay graph with applications to routeing in mobile networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-18
- Print publication:
- March 2000
-
- Article
- Export citation
Phase transition in the random triangle model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1101-1115
- Print publication:
- December 1999
-
- Article
- Export citation
Asymptotics of pooling design performance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 951-964
- Print publication:
- December 1999
-
- Article
- Export citation
The central limit theorem for Euclidean minimal spanning trees II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 969-984
- Print publication:
- December 1999
-
- Article
- Export citation
Asymptotic properties of the connectivity number of random railways
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 720-741
- Print publication:
- September 1999
-
- Article
- Export citation
On the size of a random sphere of influence graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 596-609
- Print publication:
- September 1999
-
- Article
- Export citation
Epidemic processes on digraphs of random mappings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 780-798
- Print publication:
- September 1999
-
- Article
- Export citation
Asymptotics for geometric location problems over random samples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 632-642
- Print publication:
- September 1999
-
- Article
- Export citation
The random triangle model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 852-867
- Print publication:
- September 1999
-
- Article
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation
Fractal n-hedral tilings of ℝd
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-417
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Explicit sufficient invariants for an interacting particle system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 633-641
- Print publication:
- September 1998
-
- Article
- Export citation
Extremes for the minimal spanning tree on normally distributed points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 628-639
- Print publication:
- September 1998
-
- Article
- Export citation
Approximate upper bounds for the critical probability of oriented percolation in two dimensions based on rapidly mixing Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 859-867
- Print publication:
- December 1997
-
- Article
- Export citation
Pascal's triangles in Abelian and hyperbolic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-288
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
The Minimum Vertex Degree of a Graph on Uniform Points in [0, 1]d
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 582-594
- Print publication:
- September 1997
-
- Article
- Export citation
The Maximum Vertex Degree of a Graph on Uniform Points in [0, 1]d
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 567-581
- Print publication:
- September 1997
-
- Article
- Export citation
A new proof of the Macdonald identities for An−1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-360
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
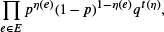
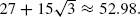 It is furthermore demonstrated that phase transition cannot occur unless
It is furthermore demonstrated that phase transition cannot occur unless