Refine listing
Actions for selected content:
1718 results in 05xxx
HYPER-WIENER INDEX OF ZIGZAG POLYHEX NANOTUBES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 75-86
-
- Article
-
- You have access
- Export citation
MINORS IN WEIGHTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 455-464
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
CUBIC EDGE-TRANSITIVE GRAPHS OF ORDER 8p2
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 315-323
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF INDEPENDENT SETS FOR (a,b,k)-CRITICAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 277-283
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON THE HU–HWANG–WANG CONJECTURE FOR GROUP TESTING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 561-571
-
- Article
-
- You have access
- Export citation
On the number of jumps of random walks with a barrier
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 206-228
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Local properties of random mappings with exchangeable in-degrees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 183-205
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Bisymmetric functions, Macdonald polynomials and
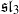 basic hypergeometric series
basic hypergeometric series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 271-303
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
INDECOMPOSABILITY GRAPHS OF RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 151-159
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
On the connectivity and diameter of small-world networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 853-863
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Graphs with specified degree distributions, simple epidemics, and local vaccination strategies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 922-948
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Counterexamples to Okounkov’s log-concavity conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1545-1557
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
CLT-related large deviation bounds based on Stein's method
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 731-752
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Coupling of Two SIR Epidemic Models with Variable Susceptibilities and Infectivities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 41-57
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Large Deviations Principle for Occupancy Problems with Colored Balls
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-141
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On the asymptotic behaviour of random recursive trees in random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1047-1070
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
An urn model arising from all-optical networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 952-966
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Cubic symmetric graphs of order twice an odd prime-power
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-164
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Large deviations-based upper bounds on the expected relative length of longest common subsequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 827-852
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Efficient routeing in Poisson small-world networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 678-686
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
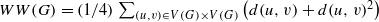 , where
, where 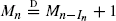 for
for 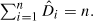 In the random digraph,
In the random digraph,  basic hypergeometric series
basic hypergeometric series
