Refine listing
Actions for selected content:
1718 results in 05xxx
CLOSED FORM FORMULA FOR THE NUMBER OF RESTRICTED COMPOSITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 289-297
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
TOPOLOGY OF INTERCONNECTION NETWORKS WITH GIVEN DEGREE AND DIAMETER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 350-352
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
ON EMBEDDINGS OF FINITE METRIC SPACES IN ln∞
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 135-139
- Print publication:
- January 2010
-
- Article
- Export citation
DIRECTED SIMPLICES IN HIGHER ORDER TOURNAMENTS
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 173-181
- Print publication:
- January 2010
-
- Article
- Export citation
PERMUTATION CLASSES OF EVERY GROWTH RATE ABOVE 2.48188
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 182-192
- Print publication:
- January 2010
-
- Article
- Export citation
On the number of allelic types for samples taken from exchangeable coalescents with mutation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1082-1101
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
On the Degree Sequence of an Evolving Random Graph Process and Its Critical Phenomenon
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1213-1220
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
MUTUALLY ORTHOGONAL FAMILIES OF LINEAR SUDOKU SOLUTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 409-420
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Isomorphism and Symmetries in Random Phylogenetic Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1005-1019
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Noncrossing partitions and representations of quivers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1533-1562
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
ON POINT SETS IN VECTOR SPACES OVER FINITE FIELDS THAT DETERMINE ONLY ACUTE ANGLE TRIANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 21 October 2009, pp. 114-120
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
DECOMPOSITIONS OF GENERALIZED COMPLETE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 October 2009, pp. 523-525
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
ON THE ORDER OF ARC-STABILIZERS IN ARC-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 October 2009, pp. 498-505
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Threshold behaviour and final outcome of an epidemic on a random network with household structure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 765-796
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Large deviations for the leaves in some random trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 845-873
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
ON MAXIMAL ENERGY AND HOSOYA INDEX OF TREES WITHOUT PERFECT MATCHING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 27 July 2009, pp. 47-57
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
A NEW CHARACTERIZATION OF WIMAN SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 360-368
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
THE TILING SEMIGROUPS OF ONE-DIMENSIONAL PERIODIC TILINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 23 July 2009, pp. 153-160
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Random hypergraphs in pseudofinite fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 03 June 2009, pp. 29-47
- Print publication:
- January 2010
-
- Article
- Export citation
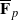 -representation
-representation 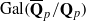 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(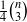 directed triangles, and that the constant
directed triangles, and that the constant  is best possible. Motivated by some geometric considerations, our aim in this paper is to consider some “higher order” versions of this statement. For example, if we give each 3-set from an
is best possible. Motivated by some geometric considerations, our aim in this paper is to consider some “higher order” versions of this statement. For example, if we give each 3-set from an  ,
,  and
and 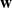 in the
in the 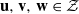 define acute angle triangles. A similar question in the real space ℛ
define acute angle triangles. A similar question in the real space ℛ