Refine listing
Actions for selected content:
1718 results in 05xxx
Asymptotic Properties of a Leader Election Algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 569-575
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Generalizations of Clausen's Formula and algebraic transformations of Calabi–Yau differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 273-295
-
- Article
-
- You have access
- Export citation
Optimal paths on the space-time SINR random graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 131-150
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
A weakly 1-stable distribution for the number of random records and cuttings in split trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 151-177
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Generalized Coupon Collection: The Superlinear Case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 189-199
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Mixing properties for STIT tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 40-48
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Cubic graphs admitting transitive non-abelian characteristically simple groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 113-123
-
- Article
-
- You have access
- Export citation
SIMPLE EXTENSIONS OF COMBINATORIAL STRUCTURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 193-214
- Print publication:
- July 2011
-
- Article
- Export citation
ON THE PARTITION MONOID AND SOME RELATED SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 273-288
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Large Cliques in a Power-Law Random Graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1124-1135
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Critical epidemics, random graphs, and Brownian motion with a parabolic drift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1187-1206
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Random Networks with Preferential Growth and Vertex Death
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1150-1163
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Gaussian phases in generalized coupon collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 994-1012
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
NONEXISTENCE OF A CIRCULANT EXPANDER FAMILY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 87-95
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
ON A COMBINATORIAL PROOF FOR AN IDENTITY INVOLVING THE TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 46-49
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Criticality of the exponential rate of decay for the largest nearest-neighbor link in random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 631-658
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Extreme value theory, Poisson-Dirichlet distributions, and first passage percolation on random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 706-738
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Phases in the Diffusion of Gases via the Ehrenfest URN Modelx
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 841-855
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Poisson Approximation of the Number of Cliques in Random Intersection Graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 826-840
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Gibbs Random Fields with Unbounded Spins on Unbounded Degree Graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-875
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
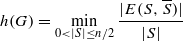
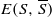 denotes the set of edges in
denotes the set of edges in 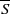 . An expander family is a sequence {
. An expander family is a sequence {