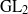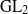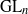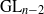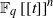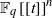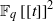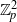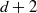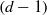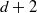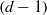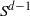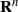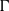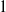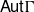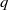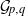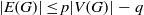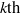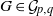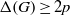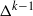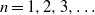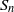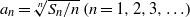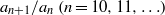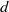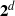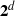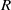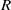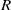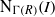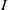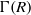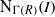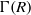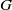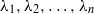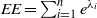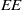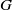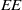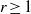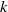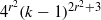Refine listing
Actions for selected content:
1718 results in 05xxx
TILING BRANCHING MULTIPLICITY SPACES WITH GL
 ${}_{2} $ PATTERN BLOCKS
${}_{2} $ PATTERN BLOCKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 362-374
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
KAKEYA SETS OVER NON-ARCHIMEDEAN LOCAL RINGS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 257-266
- Print publication:
- July 2013
-
- Article
- Export citation
ALMOST ALL SETS OF
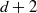 $d+ 2$ POINTS ON THE
$d+ 2$ POINTS ON THE 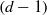 $(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
$(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 267-268
- Print publication:
- July 2013
-
- Article
- Export citation
1-REGULAR CAYLEY GRAPHS OF VALENCY 7
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 479-485
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON THE SUM OF POWERS OF THE DEGREES OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 353-358
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Connectivity of Random Geometric Graphs Related to Minimal Spanning Forests
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 20-36
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Full- and Half-Gilbert Tessellations with Rectangular Cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1-19
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
ELUSIVE CODES IN HAMMING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 286-296
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
BOUNDS ON MINORS OF BINARY MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 23 December 2012, pp. 280-285
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
WIENER INDEX AND TRACEABLE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 380-383
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Bases for cluster algebras from surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 07 December 2012, pp. 217-263
- Print publication:
- February 2013
-
- Article
- Export citation
The string of nets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 223-262
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 01 March 2013, pp. 259-276
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Maximizing the Size of the Giant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1156-1165
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Proof of a positivity conjecture of M. Kontsevich on non-commutative cluster variables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1821-1832
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
ON THE REGULAR DIGRAPH OF IDEALS OF COMMUTATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 177-189
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
ESTRADA INDEX OF GENERAL WEIGHTED GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 28 September 2012, pp. 106-112
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
NOTE ON ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 448-451
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA: COMPUTATION AND REAL EHRHART THEORY
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 05 September 2012, pp. 1-22
- Print publication:
- January 2013
-
- Article
- Export citation