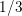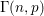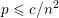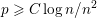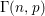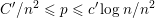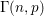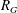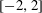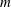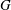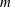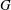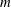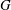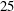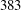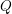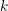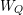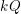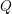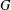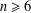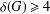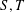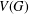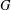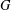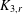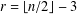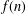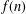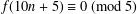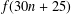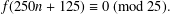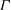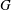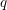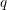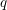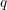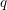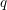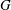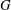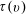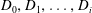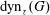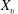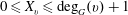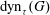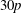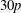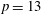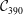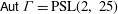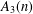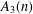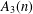Refine listing
Actions for selected content:
1718 results in 05xxx
Continuum AB percolation and AB random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 333-344
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Asymptotic hitting probabilities for the Bolthausen-Sznitman coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 87-97
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Percolation on the Information-Theoretically Secure Signal to Interference Ratio Graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 910-920
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The probability that a random multigraph is simple. II
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 123-137
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Random triangular groups at density
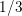 $1/3$
$1/3$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 167-178
- Print publication:
- January 2015
-
- Article
- Export citation
EXPANSION CONSTANTS AND HYPERBOLIC EMBEDDINGS OF FINITE GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 19 November 2014, pp. 1-13
- Print publication:
- January 2015
-
- Article
- Export citation
A classification of all 1-Salem graphs
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 November 2014, pp. 582-594
-
- Article
-
- You have access
- Export citation
ROW CONVEX TABLEAUX AND BOTT–SAMELSON VARIETIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 23 October 2014, pp. 315-330
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Quotient closed subcategories of quiver representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 568-602
- Print publication:
- March 2015
-
- Article
- Export citation
A NOTE ON ALMOST BALANCED BIPARTITIONS OF A GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 177-182
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
ESTIMATION AND COMPUTATION WITH MATRICES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 175-176
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A NEW CONGRUENCE MODULO 25 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 41-46
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
CANONICAL REPRESENTATIVES FOR DIVISOR CLASSES ON TROPICAL CURVES AND THE MATRIX–TREE THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 26 September 2014, e24
-
- Article
-
- You have access
- Open access
- Export citation
FINITE 3-GEODESIC TRANSITIVE BUT NOT 3-ARC TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 183-190
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Spectral theory for the
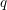 $q$-Boson particle system
$q$-Boson particle system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 1-67
- Print publication:
- January 2015
-
- Article
- Export citation
ON DYNAMIC MONOPOLIES OF GRAPHS WITH PROBABILISTIC THRESHOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 363-375
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Minimal Clade Size in the Bolthausen-Sznitman Coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 657-668
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Invariant Bipartite Random Graphs on Rd
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 769-779
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
PENTAVALENT SYMMETRIC GRAPHS OF ORDER
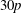 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}30p$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 353-362
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
INFINITE FAMILIES OF CONGRUENCES MODULO 3 AND 9 FOR BIPARTITIONS WITH 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 August 2014, pp. 47-52
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
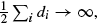 the probability that the multigraph is simple stays away from 0 if and only if
the probability that the multigraph is simple stays away from 0 if and only if 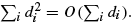 The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.
The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.