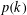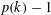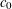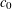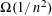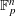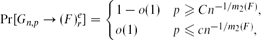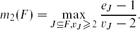Refine listing
Actions for selected content:
1718 results in 05xxx
First-Order Convergence and Roots†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 24 February 2015, pp. 213-221
-
- Article
- Export citation
The (7, 4)-Conjecture in Finite Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 10 February 2015, pp. 680-686
-
- Article
- Export citation
SHUTOUT GAMES ON GRAPHS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 03 February 2015, pp. 523-530
- Print publication:
- September 2015
-
- Article
- Export citation
Easily Testable Graph Properties
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 02 February 2015, pp. 646-657
-
- Article
- Export citation
A Numerical Lower Bound for the Spectral Radius of Random Walks on Surface Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 838-856
-
- Article
- Export citation
Lazy Cops and Robbers on Hypercubes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 829-837
-
- Article
- Export citation
On the Length of a Random Minimum Spanning Tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 23 January 2015, pp. 89-107
-
- Article
- Export citation
Partial Shadows of Set Systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 20 January 2015, pp. 825-828
-
- Article
- Export citation
EIGENVALUES AND LINEAR QUASIRANDOM HYPERGRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 January 2015, e2
-
- Article
-
- You have access
- Open access
- Export citation
Combinatorial Structures on van der Waerden sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 929-953
-
- Article
- Export citation
The Sharp Threshold for Maximum-Size Sum-Free Subsets in Even-Order Abelian Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 609-640
-
- Article
- Export citation
PRIMITIVE RECURSIVE BOUNDS FOR THE FINITE VERSION OF GOWERS’
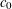 $c_{0}$ THEOREM
$c_{0}$ THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 501-522
- Print publication:
- September 2015
-
- Article
- Export citation
ON CONFIGURATIONS WHERE THE LOOMIS–WHITNEY INEQUALITY IS NEARLY SHARP AND APPLICATIONS TO THE FURSTENBERG SET PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 145-161
- Print publication:
- January 2015
-
- Article
- Export citation
Decomposing Random Graphs into Few Cycles and Edges
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 December 2014, pp. 857-872
-
- Article
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
A Short Proof of the Random Ramsey Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 22 December 2014, pp. 130-144
-
- Article
- Export citation
Minimum Number of Monotone Subsequences of Length 4 in Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 19 December 2014, pp. 658-679
-
- Article
- Export citation
ADVENTURES IN INVARIANT THEORY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 105-115
-
- Article
-
- You have access
- Export citation
The front of the epidemic spread and first passage percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 101-121
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
How Clustering Affects Epidemics in Random Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 985-1008
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation