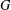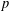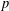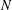Refine listing
Actions for selected content:
1765 results in 05xxx
Probabilistic Divide-and-Conquer: A New Exact Simulation Method, With Integer Partitions as an Example
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 324-351
-
- Article
- Export citation
THE LEVEL 12 ANALOGUE OF RAMANUJAN’S FUNCTION
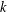 $k$
$k$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-53
-
- Article
-
- You have access
- Export citation
Minimum Degrees and Codegrees of Ramsey-Minimal 3-Uniform Hypergraphs* †
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 850-869
-
- Article
- Export citation
The Inversion Number and the Major Index are Asymptotically Jointly Normally Distributed on Words
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 14 January 2016, pp. 470-483
-
- Article
- Export citation
Generalized friezes and a modified Caldero–Chapoton map depending on a rigid object
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-124
-
- Article
-
- You have access
- Export citation
A 2-ARC TRANSITIVE PENTAVALENT CAYLEY GRAPH OF
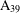 $\text{A}_{39}$
$\text{A}_{39}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 441-446
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA II: BIDEGREE AND POISSON FORMULA
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 653-684
- Print publication:
- 2016
-
- Article
- Export citation
ORTHOGONAL COLORINGS OF THE SPHERE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 04 February 2016, pp. 492-501
- Print publication:
- 2016
-
- Article
- Export citation
A NOTE ON RANDOM MATRIX INTEGRALS, MOMENT IDENTITIES, AND CATALAN NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 811-817
- Print publication:
- 2016
-
- Article
- Export citation
LOWER BOUND THEOREMS AND A GENERALIZED LOWER BOUND CONJECTURE FOR BALANCED SIMPLICIAL COMPLEXES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 441-477
- Print publication:
- 2016
-
- Article
- Export citation
UPPER BOUND THEOREM FOR ODD-DIMENSIONAL FLAG TRIANGULATIONS OF MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 909-928
- Print publication:
- 2016
-
- Article
- Export citation
The Multiple-Orientability Thresholds for Random Hypergraphs†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 28 December 2015, pp. 870-908
-
- Article
- Export citation
Manipulative Waiters with Probabilistic Intuition
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 823-849
-
- Article
- Export citation
Local Maxima of Quadratic Boolean Functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 633-640
-
- Article
- Export citation
Path Ramsey Number for Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 612-622
-
- Article
- Export citation
Contagions in random networks with overlapping communities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 973-988
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
The extinction time of a subcritical branching process related to the SIR epidemic on a random graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1195-1201
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On a generalization of a waiting time problem and some combinatorial identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 981-989
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
-
- Article
-
- You have access
- Export citation
UNIMODALITY AND COLOURED HOOK FACTORISATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 1-12
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
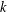
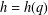
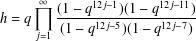
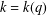
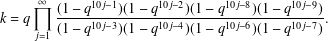
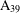
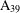
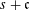


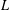

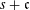
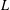

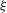

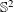
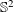
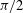
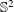
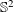
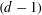
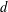
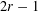
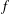
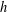
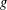
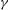

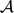
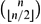
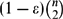
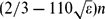
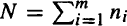 Let
Let