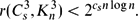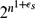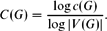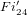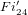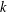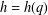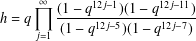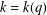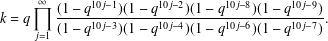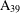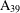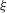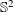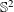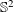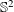Refine listing
Actions for selected content:
1718 results in 05xxx
Cycles and Matchings in Randomly Perturbed Digraphs and Hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 909-927
-
- Article
- Export citation
Improved Bounds for the Ramsey Number of Tight Cycles Versus Cliques
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 791-796
-
- Article
- Export citation
Application of Braiding Sequences. II. Polynomial Invariants of Positive Knots
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 1037-1064
-
- Article
- Export citation
On the Normalized Shannon Capacity of a Union
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 766-767
-
- Article
- Export citation
Computing cup products in integral cohomology ofHilbert schemes of points on K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 78-97
-
- Article
-
- You have access
- Export citation
Secrecy coverage in two dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 1-12
- Print publication:
- March 2016
-
- Article
- Export citation
Structure of the
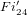 $Fi_{24}^{\prime }$ maximal
$Fi_{24}^{\prime }$ maximal  $2$ -local geometry point-line collinearity graph
$2$ -local geometry point-line collinearity graph
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 105-154
-
- Article
-
- You have access
- Export citation
SELECTED TOPICS IN SPECTRAL GRAPH THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 511-512
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON ARC-REGULAR FROBENIUS METACIRCULANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 20-29
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Coexistence in Preferential Attachment Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 09 February 2016, pp. 797-822
-
- Article
- Export citation
Inapproximability of the Partition Function for the Antiferromagnetic Ising and Hard-Core Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 500-559
-
- Article
- Export citation
CAYLEY GRAPHS OVER A FINITE CHAIN RING AND GCD-GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 353-363
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Probabilistic Divide-and-Conquer: A New Exact Simulation Method, With Integer Partitions as an Example
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 324-351
-
- Article
- Export citation
THE LEVEL 12 ANALOGUE OF RAMANUJAN’S FUNCTION
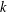 $k$
$k$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Minimum Degrees and Codegrees of Ramsey-Minimal 3-Uniform Hypergraphs* †
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 850-869
-
- Article
- Export citation
The Inversion Number and the Major Index are Asymptotically Jointly Normally Distributed on Words
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 14 January 2016, pp. 470-483
-
- Article
- Export citation
A 2-ARC TRANSITIVE PENTAVALENT CAYLEY GRAPH OF
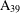 $\text{A}_{39}$
$\text{A}_{39}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 441-446
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA II: BIDEGREE AND POISSON FORMULA
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 653-684
- Print publication:
- 2016
-
- Article
- Export citation
ORTHOGONAL COLORINGS OF THE SPHERE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 04 February 2016, pp. 492-501
- Print publication:
- 2016
-
- Article
- Export citation
A NOTE ON RANDOM MATRIX INTEGRALS, MOMENT IDENTITIES, AND CATALAN NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 811-817
- Print publication:
- 2016
-
- Article
- Export citation