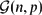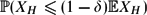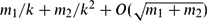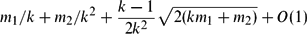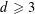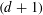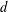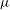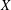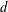Refine listing
Actions for selected content:
1718 results in 05xxx
The Threshold Probability for Long Cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 08 September 2016, pp. 208-247
-
- Article
- Export citation
Longest paths in random Apollonian networks and largest r-ary subtrees of random d-ary recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 846-856
- Print publication:
- September 2016
-
- Article
- Export citation
Degrees and distances in random and evolving apollonian networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 865-902
- Print publication:
- September 2016
-
- Article
- Export citation
On the relation between graph distance and Euclidean distance in random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 848-864
- Print publication:
- September 2016
-
- Article
- Export citation
WIENER INDEX ON TRACEABLE AND HAMILTONIAN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 362-372
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Triangles in Cartesian Squares of Quasirandom Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 25 August 2016, pp. 161-182
-
- Article
- Export citation
On the Lower Tail Variational Problem for Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 16 August 2016, pp. 301-320
-
- Article
- Export citation
Judicious Partitioning of Hypergraphs with Edges of Size at Most 2†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 16 August 2016, pp. 267-284
-
- Article
- Export citation
COMPLEX NETWORK TOOLS TO ENABLE IDENTIFICATION OF A CRIMINAL COMMUNITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 350-352
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
On the Widom–Rowlinson Occupancy Fraction in Regular Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 09 August 2016, pp. 183-194
-
- Article
- Export citation
THERE ARE ASYMPTOTICALLY THE SAME NUMBER OF LATIN SQUARES OF EACH PARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 187-194
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Asymptotic normality of degree counts in a preferential attachment model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 283-299
- Print publication:
- July 2016
-
- Article
- Export citation
INVARIANT MEASURES CONCENTRATED ON COUNTABLE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 28 June 2016, e17
-
- Article
-
- You have access
- Open access
- Export citation
BROOKS’ THEOREM FOR MEASURABLE COLORINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 24 June 2016, e16
-
- Article
-
- You have access
- Open access
- Export citation
Large Unavoidable Subtournaments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 21 June 2016, pp. 68-77
-
- Article
- Export citation
Median Eigenvalues of Bipartite Subcubic Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 768-790
-
- Article
- Export citation
A Determinant Identity Implying the Lagrange–Good Inversion Formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 165-176
-
- Article
- Export citation
DISTRIBUTIVE LATTICES OF TILTING MODULES AND SUPPORT τ-TILTING MODULES OVER PATH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 503-511
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
A TOPOLOGICAL VARIATION OF THE RECONSTRUCTION CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 221-235
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 07 June 2016, pp. 165-166
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation