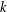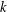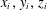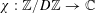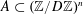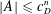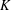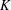Refine listing
Actions for selected content:
1718 results in 05xxx
Anagram-Free Colourings of Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 08 August 2017, pp. 623-642
-
- Article
- Export citation
Diameter of the Stochastic Mean-Field Model of Distance
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 797-825
-
- Article
- Export citation
Induced Subgraphs With Many Distinct Degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 01 August 2017, pp. 110-123
-
- Article
- Export citation
Maximal Steiner Trees in the Stochastic Mean-Field Model of Distance
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 826-838
-
- Article
- Export citation
UPPER BOUNDS FOR SUNFLOWER-FREE SETS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 June 2017, e15
-
- Article
-
- You have access
- Open access
- Export citation
EQUIVARIANT
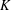 $K$ -THEORY OF GRASSMANNIANS
$K$ -THEORY OF GRASSMANNIANS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 June 2017, e3
-
- Article
-
- You have access
- Open access
- Export citation
Fractional Clique Decompositions of Dense Partite Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 911-943
-
- Article
- Export citation
TWO NEW LOWER BOUNDS FOR THE SPARK OF A MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 353-360
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Corners Over Quasirandom Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 944-951
-
- Article
- Export citation
On the Maximum Number of Spanning Copies of an Orientation in a Tournament
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 06 June 2017, pp. 775-796
-
- Article
- Export citation
Joint degree distributions of preferential attachment random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 368-387
- Print publication:
- June 2017
-
- Article
- Export citation
Convex Polygons in Geometric Triangulations†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 30 May 2017, pp. 641-659
-
- Article
- Export citation
Critical Window for Connectivity in the Configuration Model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 29 May 2017, pp. 660-680
-
- Article
- Export citation
The Proofs of Two Directed Paths Conjectures of Bollobás and Leader
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 22 May 2017, pp. 762-774
-
- Article
- Export citation
Bridge-Addability, Edge-Expansion and Connectivity
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 11 May 2017, pp. 697-719
-
- Article
- Export citation
Comparing Graphs of Different Sizes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 5 / September 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 681-696
-
- Article
- Export citation
ISOLATED SCATTERING NUMBER OF SPLIT GRAPHS AND GRAPH PRODUCTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 12 April 2017, pp. 350-358
-
- Article
-
- You have access
- Export citation
Stability and Turán Numbers of a Class of Hypergraphs via Lagrangians
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 367-405
-
- Article
- Export citation
SOME RESULTS ON AN ALGEBRO-GEOMETRIC CONDITION ON GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 29 March 2017, pp. 218-254
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
An Inequality for Functions on the Hamming Cube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 468-480
-
- Article
- Export citation