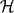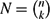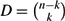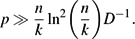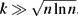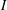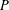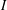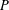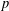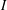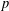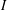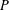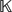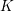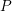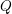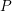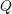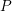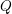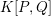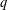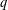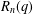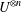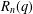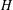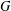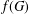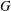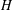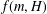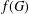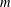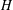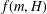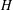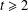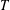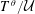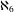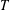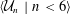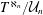Refine listing
Actions for selected content:
1718 results in 05xxx
Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 406-422
-
- Article
- Export citation
UNDECIDABILITY AND THE DEVELOPABILITY OF PERMUTOIDS AND RIGID PSEUDOGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 March 2017, e10
-
- Article
-
- You have access
- Open access
- Export citation
THE EXPECTED JAGGEDNESS OF ORDER IDEALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 March 2017, e9
-
- Article
-
- You have access
- Open access
- Export citation
ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 14 March 2017, pp. 705-715
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Equivariant
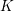 $K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
$K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 09 March 2017, pp. 667-677
- Print publication:
- April 2017
-
- Article
- Export citation
ISOTONIAN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 March 2017, pp. 83-101
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
A Stability Result for Families with Fixed Diameter
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 506-516
-
- Article
- Export citation
THE ANNIHILATOR OF TENSOR SPACE IN THE
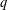 $q$ -ROOK MONOID ALGEBRA
$q$ -ROOK MONOID ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 77-86
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
On the asymptotics of constrained exponential random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 165-180
- Print publication:
- March 2017
-
- Article
- Export citation
Local limits of Galton–Watson trees conditioned on the number of protected nodes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 55-65
- Print publication:
- March 2017
-
- Article
- Export citation
On the treewidth of random geometric graphs and percolated grids
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 49-60
- Print publication:
- March 2017
-
- Article
- Export citation
From coin tossing to rock-paper-scissors and beyond: a log-exp gap theorem for selecting a leader
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 213-235
- Print publication:
- March 2017
-
- Article
- Export citation
Nonuniversality of weighted random graphs with infinite variance degree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 146-164
- Print publication:
- March 2017
-
- Article
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Shearer's point process, the hard-sphere model, and a continuum Lovász local lemma
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 1-23
- Print publication:
- March 2017
-
- Article
- Export citation
Geometric-progression-free sets over quadratic number fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 245-262
- Print publication:
- April 2017
-
- Article
- Export citation
BIPARTITE SUBGRAPHS OF
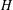 $H$ -FREE GRAPHS
$H$ -FREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 1-13
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
A Rainbow r-Partite Version of the Erdős–Ko–Rado Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 23 January 2017, pp. 321-337
-
- Article
- Export citation
REDUCED POWERS OF SOUSLIN TREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 January 2017, e2
-
- Article
-
- You have access
- Open access
- Export citation
TOPOLOGY OF COMPLEX NETWORKS: MODELS AND ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 347-349
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation