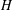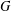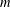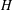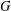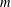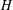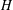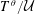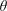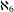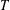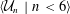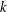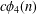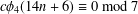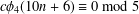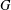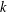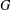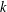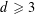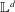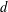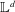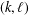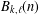Refine listing
Actions for selected content:
1766 results in 05xxx
From coin tossing to rock-paper-scissors and beyond: a log-exp gap theorem for selecting a leader
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 213-235
- Print publication:
- March 2017
-
- Article
- Export citation
Nonuniversality of weighted random graphs with infinite variance degree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 146-164
- Print publication:
- March 2017
-
- Article
- Export citation
THE IDEMPOTENT-GENERATED SUBSEMIGROUP OF THE KAUFFMAN MONOID
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 673-683
-
- Article
-
- You have access
- Export citation
Shearer's point process, the hard-sphere model, and a continuum Lovász local lemma
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 1-23
- Print publication:
- March 2017
-
- Article
- Export citation
Geometric-progression-free sets over quadratic number fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 245-262
- Print publication:
- April 2017
-
- Article
- Export citation
BIPARTITE SUBGRAPHS OF
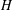 $H$ -FREE GRAPHS
$H$ -FREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 1-13
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
A Rainbow r-Partite Version of the Erdős–Ko–Rado Theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 23 January 2017, pp. 321-337
-
- Article
- Export citation
REDUCED POWERS OF SOUSLIN TREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 January 2017, e2
-
- Article
-
- You have access
- Open access
- Export citation
TOPOLOGY OF COMPLEX NETWORKS: MODELS AND ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 347-349
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
On the Number of 4-Edge Paths in Graphs With Given Edge Density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 431-447
-
- Article
- Export citation
CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 157-176
-
- Article
-
- You have access
- Export citation
DICHROMATIC NUMBER AND FRACTIONAL CHROMATIC NUMBER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 15 December 2016, e32
-
- Article
-
- You have access
- Open access
- Export citation
Existence of Spanning ℱ-Free Subgraphs with Large Minimum Degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 448-467
-
- Article
- Export citation
Planting Colourings Silently
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 338-366
-
- Article
- Export citation
ON THE STRUCTURE OF GRAPHS WHICH ARE LOCALLY INDISTINGUISHABLE FROM A LATTICE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 December 2016, e31
-
- Article
-
- You have access
- Open access
- Export citation
The deterministic Kermack‒McKendrick model bounds the general stochastic epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1031-1040
- Print publication:
- December 2016
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF
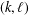 $(k,\ell )$ -REGULAR BIPARTITIONS
$(k,\ell )$ -REGULAR BIPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 353-364
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
On the evolution of topology in dynamic clique complexes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 989-1014
- Print publication:
- December 2016
-
- Article
- Export citation
Stability of the stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1064-1077
- Print publication:
- December 2016
-
- Article
- Export citation
Local Conditions for Exponentially Many Subdivisions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 28 November 2016, pp. 423-430
-
- Article
- Export citation