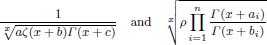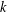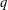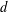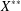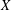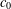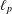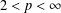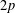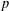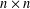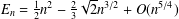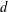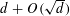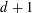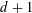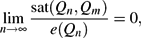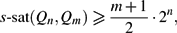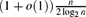Refine listing
Actions for selected content:
1718 results in 05xxx
On the Number of 4-Edge Paths in Graphs With Given Edge Density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 431-447
-
- Article
- Export citation
CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 157-176
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
DICHROMATIC NUMBER AND FRACTIONAL CHROMATIC NUMBER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 15 December 2016, e32
-
- Article
-
- You have access
- Open access
- Export citation
Existence of Spanning ℱ-Free Subgraphs with Large Minimum Degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 448-467
-
- Article
- Export citation
Planting Colourings Silently
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 338-366
-
- Article
- Export citation
ON THE STRUCTURE OF GRAPHS WHICH ARE LOCALLY INDISTINGUISHABLE FROM A LATTICE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 December 2016, e31
-
- Article
-
- You have access
- Open access
- Export citation
The deterministic Kermack‒McKendrick model bounds the general stochastic epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1031-1040
- Print publication:
- December 2016
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF
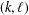 $(k,\ell )$ -REGULAR BIPARTITIONS
$(k,\ell )$ -REGULAR BIPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 353-364
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
On the evolution of topology in dynamic clique complexes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 989-1014
- Print publication:
- December 2016
-
- Article
- Export citation
Stability of the stochastic matching model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1064-1077
- Print publication:
- December 2016
-
- Article
- Export citation
Local Conditions for Exponentially Many Subdivisions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 3 / May 2017
- Published online by Cambridge University Press:
- 28 November 2016, pp. 423-430
-
- Article
- Export citation
COMPACT SPACES OF THE FIRST BAIRE CLASS THAT HAVE OPEN FINITE DEGREE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 21 November 2016, pp. 1173-1196
- Print publication:
- November 2018
-
- Article
- Export citation
The Monotonicity and Log-Behaviour of Some Functions Related to the Euler Gamma Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 November 2016, pp. 527-543
-
- Article
- Export citation
FINITELY DEPENDENT COLORING
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 03 November 2016, e9
-
- Article
-
- You have access
- Open access
- Export citation
COMPARING THE GENERALISED ROUNDNESS OF METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 299-314
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
RAMANUJAN CAYLEY GRAPHS OF FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 373-383
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
THE DIMENSION OF CENTRALISERS OF MATRICES OF ORDER
 $n$
$n$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 353-361
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
KŐNIG’S LINE COLORING AND VIZING’S THEOREMS FOR GRAPHINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 September 2016, e27
-
- Article
-
- You have access
- Open access
- Export citation
Saturated Subgraphs of the Hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 52-67
-
- Article
- Export citation
On the Chromatic Number of Random Cayley Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 248-266
-
- Article
- Export citation
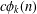
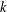

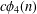
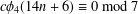
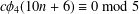
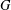
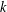
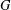
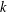

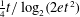
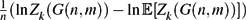
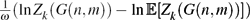
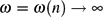
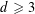
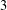
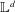
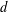
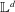
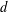
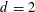
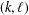
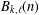
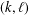

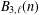
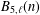


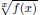 is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions
is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions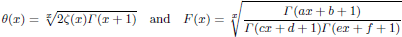
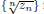 for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients
for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients 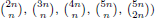 are demonstrated. In particular, this contains some results of Chen
are demonstrated. In particular, this contains some results of Chen 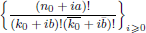
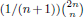 and the central binomial coefficients
and the central binomial coefficients 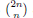 are infinitely log-monotonic, and strengthens one result of Su and Wang that
are infinitely log-monotonic, and strengthens one result of Su and Wang that 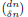 is log-convex in
is log-convex in