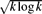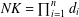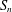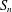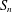Refine listing
Actions for selected content:
1718 results in 05xxx
INTERPOLATED SCHUR MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 25 October 2017, pp. 289-307
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Arithmetic properties of Apéry-like numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 249-274
- Print publication:
- February 2018
-
- Article
- Export citation
DIAGRAM ALGEBRAS, DOMINANCE TRIANGULARITY AND SKEW CELL MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 13-36
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Counting Intersecting and Pairs of Cross-Intersecting Families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 60-68
-
- Article
- Export citation
Monotone Subsequences in High-Dimensional Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 69-83
-
- Article
- Export citation
On Edge-Disjoint Spanning Trees in a Randomly Weighted Complete Graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 228-244
-
- Article
- Export citation
Colourings of Uniform Hypergraphs with Large Girth and Applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 245-273
-
- Article
- Export citation
SOME NEW LOWER BOUNDS FOR THE KIRCHHOFF INDEX OF A GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 1-10
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
LOW-DEGREE BOOLEAN FUNCTIONS ON
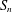 $S_{n}$ , WITH AN APPLICATION TO ISOPERIMETRY
$S_{n}$ , WITH AN APPLICATION TO ISOPERIMETRY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 03 October 2017, e23
-
- Article
-
- You have access
- Open access
- Export citation
Bisections of Graphs Without Short Cycles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 44-59
-
- Article
- Export citation
SIMPLE GROUPS, PRODUCT ACTIONS, AND GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 14 September 2017, pp. 87-126
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
A spectral method for community detection in moderately sparse degree-corrected stochastic block models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 686-721
- Print publication:
- September 2017
-
- Article
- Export citation
On a random search tree: asymptotic enumeration of vertices by distance from leaves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 850-876
- Print publication:
- September 2017
-
- Article
- Export citation
The Gini index of random trees with an application to caterpillars
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 701-709
- Print publication:
- September 2017
-
- Article
- Export citation
Computing absorbing times via fluid approximations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 768-790
- Print publication:
- September 2017
-
- Article
- Export citation
The Growth Constant of Odd Cutsets in High Dimensions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 208-227
-
- Article
- Export citation
Triangle-Free Subgraphs of Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 141-161
-
- Article
- Export citation
Generalized Majority Colourings of Digraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 850-855
-
- Article
- Export citation
Minimizing the Number of Triangular Edges
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 580-622
-
- Article
- Export citation
Log-concavity and strong q-log-convexity for Riordan arrays and recursive matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1297-1310
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation