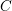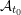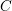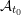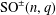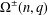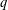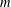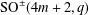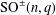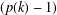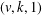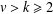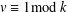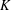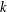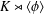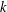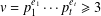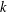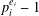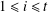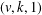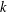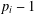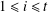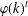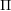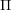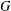Refine listing
Actions for selected content:
1738 results in 05xxx
A CONJECTURE ON
 $C$-MATRICES OF CLUSTER ALGEBRAS
$C$-MATRICES OF CLUSTER ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 19 June 2018, pp. 37-46
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Bounding the Size of an Almost-Equidistant Set in Euclidean Space
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 13 June 2018, pp. 280-286
-
- Article
- Export citation
Indistinguishable Sceneries on the Boolean Hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 05 June 2018, pp. 46-60
-
- Article
- Export citation
Spectral bounds in random graphs applied to spreading phenomena and percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 480-503
- Print publication:
- June 2018
-
- Article
- Export citation
ON INVOLUTIONS AND INDICATORS OF FINITE ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 380-416
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
RESOLVABLE MENDELSOHN DESIGNS AND FINITE FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 1-13
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Fast Property Testing and Metrics for Permutations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 24 May 2018, pp. 539-579
-
- Article
- Export citation
Eigenvalue Ratios of Non-Negatively Curved Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 23 May 2018, pp. 829-850
-
- Article
- Export citation
Generating Infinite Random Graphs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 22 May 2018, pp. 847-868
-
- Article
- Export citation
On the Number of Solutions in Random Graph k-Colouring
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 21 May 2018, pp. 130-158
-
- Article
- Export citation
Volumes in the Uniform Infinite Planar Triangulation: From Skeletons to Generating Functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 946-973
-
- Article
- Export citation
Random Recursive Trees and Preferential Attachment Trees are Random Split Trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 21 May 2018, pp. 81-99
-
- Article
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
A (5,5)-Colouring of Kn with Few Colours
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 09 May 2018, pp. 892-912
-
- Article
- Export citation
The Probability of Non-Existence of a Subgraph in a Moderately Sparse Random Graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 09 May 2018, pp. 672-715
-
- Article
- Export citation
Triangle-Tilings in Graphs Without Large Independent Sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 09 May 2018, pp. 449-474
-
- Article
- Export citation
ON THE TOTAL DISTANCE AND DIAMETER OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 14-17
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
THE COMPLEXITY OF THOMASON’S ALGORITHM FOR FINDING A SECOND HAMILTONIAN CYCLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 18-26
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Density of Chromatic Roots in Minor-Closed Graph Families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 988-998
-
- Article
- Export citation
Multicolour Sunflowers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 6 / November 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 974-987
-
- Article
- Export citation