Refine listing
Actions for selected content:
1718 results in 05xxx
Compound Poisson approximation of subgraph counts in stochastic block models with multiple edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 759-782
- Print publication:
- September 2018
-
- Article
- Export citation
Speeding up non-Markovian first-passage percolation with a few extra edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 858-886
- Print publication:
- September 2018
-
- Article
- Export citation
On extensions of van Hamme's conjectures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 1017-1027
- Print publication:
- October 2018
-
- Article
- Export citation
SYSTOLIC FILLINGS OF SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 502-511
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
COORDINATISING PLANES OF PRIME POWER ORDER USING FINITE FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 184-199
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
DETERMINING CROSSING NUMBERS OF GRAPHS OF ORDER SIX USING CYCLICPERMUTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 17 August 2018, pp. 353-362
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
GRAPH LABELLING TECHNIQUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 512-513
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
A STRUCTURED INVERSE SPECTRUM PROBLEM FOR INFINITE GRAPHS ANDUNBOUNDED OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 363-371
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Combinatorial Analysis of Growth Models for Series-Parallel Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 14 August 2018, pp. 574-599
-
- Article
- Export citation
Dual-Pivot Quicksort: Optimality, Analysis and Zeros of Associated Lattice Paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 14 August 2018, pp. 485-518
-
- Article
- Export citation
Limit Shapes via Bijections
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 02 August 2018, pp. 187-240
-
- Article
- Export citation
THE LOCAL
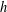 $h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
$h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 258-264
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
CONTINUOUS ASSOCIATION SCHEMES AND HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 July 2018, pp. 361-426
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Exact Distance Colouring in Trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 24 July 2018, pp. 177-186
-
- Article
- Export citation
A GENERAL POSITION PROBLEM IN GRAPH THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 177-187
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Chern class formulas for classical-type degeneracy loci
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1746-1774
- Print publication:
- August 2018
-
- Article
- Export citation
Tilings in Randomly Perturbed Dense Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 16 July 2018, pp. 159-176
-
- Article
- Export citation
Turán Number of an Induced Complete Bipartite Graph Plus an Odd Cycle
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 16 July 2018, pp. 241-252
-
- Article
- Export citation
An Extremal Graph Problem with a Transcendental Solution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 26 June 2018, pp. 303-324
-
- Article
- Export citation
On the log-concavity of the sequence
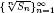 for some combinatorial sequences
for some combinatorial sequences 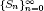
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 881-892
- Print publication:
- August 2018
-
- Article
- Export citation
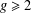
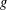
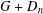
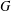
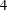
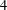
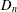

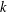
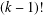
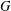
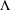
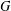
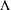
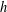
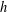
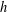
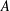
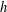
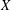
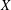
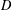
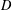
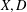
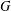
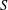
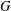
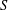
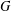
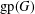
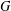
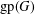
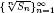 for some combinatorial sequences
for some combinatorial sequences 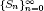
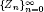 , the sequences
, the sequences 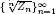 are strictly log-concave, which confirms a conjecture of Sun. We also prove the log-concavity of the sequence
are strictly log-concave, which confirms a conjecture of Sun. We also prove the log-concavity of the sequence 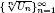 of Cohen–Rhin numbers.
of Cohen–Rhin numbers.