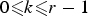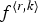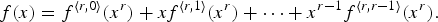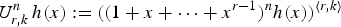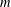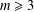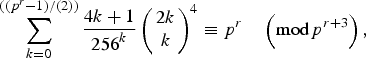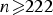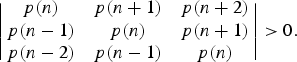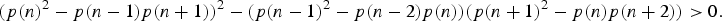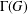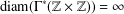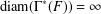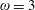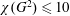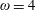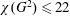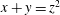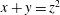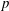Refine listing
Actions for selected content:
1718 results in 05xxx
Interlacing polynomials and the veronese construction for rational formal power series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1-16
- Print publication:
- February 2020
-
- Article
- Export citation
INTEGER POLYGONS OF GIVEN PERIMETER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 131-147
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
THE GENERALIZED ENTROPY ERGODIC THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS INDEXED BY A HOMOGENEOUS TREE
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 221-234
-
- Article
- Export citation
Some congruences involving fourth powers of central q-binomial coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1127-1138
- Print publication:
- June 2020
-
- Article
- Export citation
MONOID ACTIONS AND ULTRAFILTER METHODS IN RAMSEY THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 29 January 2019, e2
-
- Article
-
- You have access
- Open access
- Export citation
Determinantal inequalities for the partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1451-1466
- Print publication:
- June 2020
-
- Article
- Export citation
THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 68-75
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A SPECTRUM OF SERIES–PARALLEL GRAPHS WITH MULTIPLE EDGE EVOLUTION
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 487-499
-
- Article
- Export citation
Boardman–Vogt tensor products of absolutely free operads
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 367-385
- Print publication:
- February 2020
-
- Article
- Export citation
Characterization of fundamental networks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 453-474
- Print publication:
- February 2020
-
- Article
- Export citation
AN ALGORITHM TO CONSTRUCT THE LE DIAGRAM ASSOCIATED TO A GRASSMANN NECKLACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2019, pp. 85-91
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Infinite families of congruences modulo 5 and 7 for the cubic partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1189-1205
- Print publication:
- October 2019
-
- Article
- Export citation
Nonexistence of Idempotent Means on Free Binary Systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 577-581
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Colouring Squares of Claw-free Graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 113-129
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Squared Chromatic Number Without Claws or Large Cliques
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 23-35
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
A Linear Threshold for Uniqueness of Solutions to Random Jigsaw Puzzles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 08 January 2019, pp. 287-302
-
- Article
-
- You have access
- Export citation
Monochromatic Solutions to
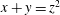 $x+y=z^{2}$
$x+y=z^{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Geometry of Uniform Spanning Forest Components in High Dimensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1297-1321
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A Boltzmann Approach to Percolation on Random Triangulations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1-43
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Flow Polytopes and the Space of Diagonal Harmonics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1495-1521
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation