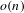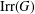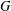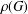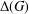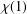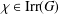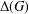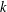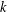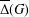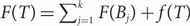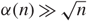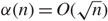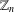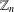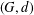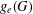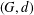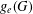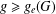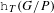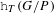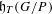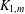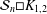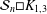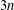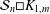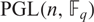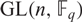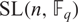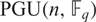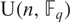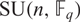Refine listing
Actions for selected content:
1718 results in 05xxx
Decomposing Graphs into Edges and Triangles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 13 March 2019, pp. 465-472
-
- Article
- Export citation
Kesten’s theorem for uniformly recurrent subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 2778-2787
- Print publication:
- October 2020
-
- Article
- Export citation
An Elementary Proof of Bevan's Theorem on the Growth of Grid Classes of Permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 975-984
-
- Article
- Export citation
ON THE REGULARITY OF CHARACTER DEGREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 428-433
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A central limit theorem for additive functionals of increasing trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 618-637
-
- Article
- Export citation
The spread of fire on a random multigraph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 1-40
- Print publication:
- March 2019
-
- Article
- Export citation
Decomposing edge-coloured graphs under colour degree constraints
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 01 March 2019, pp. 755-767
-
- Article
- Export citation
Separation Choosability and Dense Bipartite Induced Subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 26 February 2019, pp. 720-732
-
- Article
-
- You have access
- Open access
- Export citation
Restricted completion of sparse partial Latin squares
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 675-695
-
- Article
- Export citation
RAMSEY GROWTH IN SOME NIP STRUCTURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1-29
- Print publication:
- January 2021
-
- Article
- Export citation
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE RANK STATISTIC FOR STRONGLY CONCAVE COMPOSITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 230-238
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
EMBEDDING OF METRIC GRAPHS ON HYPERBOLIC SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 508-520
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
ON THE CROSSING NUMBER OF THE CARTESIAN PRODUCT OF A SUNLET GRAPH AND A STAR GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 5-12
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ORIENTED FLIP GRAPHS, NONCROSSING TREE PARTITIONS, AND REPRESENTATION THEORY OF TILING ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 147-182
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Improper colouring of graphs with no odd clique minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 04 February 2019, pp. 740-754
-
- Article
- Export citation
Limit laws of planar maps with prescribed vertex degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 04 February 2019, pp. 519-541
-
- Article
- Export citation
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 93-107
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation