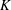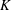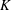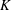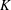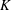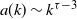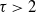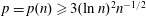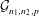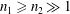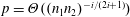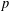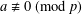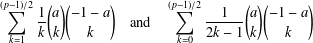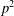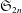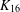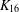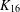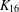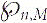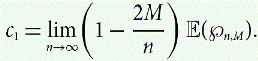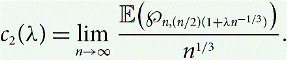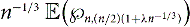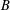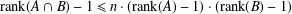Refine listing
Actions for selected content:
1718 results in 05xxx
SMALL-WORLD EFFECT IN GEOGRAPHICAL ATTACHMENT NETWORKS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 September 2019, pp. 276-296
-
- Article
- Export citation
On the Chromatic Number of Matching Kneser Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 12 September 2019, pp. 1-21
-
- Article
- Export citation
Polynomials from Combinatorial
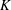 $K$-theory
$K$-theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 29-62
- Print publication:
- February 2021
-
- Article
- Export citation
Transient and slim versus recurrent and fat: Random walks and the trees they grow
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 769-786
- Print publication:
- September 2019
-
- Article
- Export citation
Degree correlations in scale-free random graph models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 672-700
- Print publication:
- September 2019
-
- Article
- Export citation
Subgraphs in preferential attachment models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 898-926
- Print publication:
- September 2019
-
- Article
- Export citation
The Genus of a Random Bipartite Graph
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 29 August 2019, pp. 1607-1623
- Print publication:
- December 2020
-
- Article
- Export citation
NEW SUPERCONGRUENCES INVOLVING PRODUCTS OF TWO BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 367-378
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
THE POLYTABLOID BASIS EXPANDS POSITIVELY INTO THE WEB BASIS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 19 August 2019, e26
-
- Article
-
- You have access
- Open access
- Export citation
BISECTORS IN VECTOR GROUPS OVER INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 15 August 2019, pp. 353-361
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ELASTIC GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e24
-
- Article
-
- You have access
- Open access
- Export citation
Quasi-Sturmian colorings on regular trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3403-3419
- Print publication:
- December 2020
-
- Article
- Export citation
CONJUGATING AUTOMORPHISMS OF GRAPH PRODUCTS: KAZHDAN’S PROPERTY (T) AND SQ-UNIVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 272-282
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
PERFECT 1-FACTORISATIONS OF
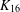 $K_{16}$
$K_{16}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 177-185
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Expected Maximum Block Size in Critical Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 25 July 2019, pp. 638-655
-
- Article
- Export citation
On Komlós’ tiling theorem in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 25 July 2019, pp. 113-127
-
- Article
- Export citation
ON A GENERALISATION OF A RESTRICTED SUM FORMULA FOR MULTIPLE ZETA VALUES AND FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 23-34
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
GENERALISATION OF A RESULT ON DISTINCT PARTITIONS WITH BOUNDED PART DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 233-237
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Enumerating coloured partitions in 2 and 3 dimensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 19 July 2019, pp. 479-505
- Print publication:
- November 2020
-
- Article
- Export citation
INTERSECTIONS OF SUBGROUPS IN VIRTUALLY FREE GROUPS AND VIRTUALLY FREE PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 266-271
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation