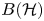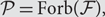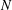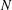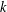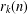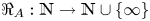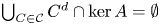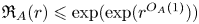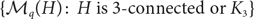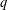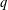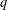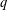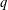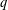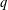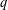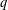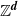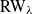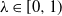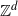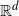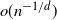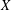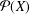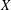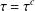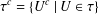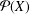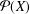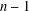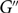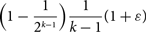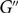Refine listing
Actions for selected content:
1718 results in 05xxx
All finite transitive graphs admit a self-adjoint free semigroupoid algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 391-406
- Print publication:
- February 2021
-
- Article
- Export citation
FRIEZE PATTERNS WITH COEFFICIENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 March 2020, e17
-
- Article
-
- You have access
- Open access
- Export citation
Estimating parameters associated with monotone properties
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 616-632
-
- Article
- Export citation
ENUMERATION OF MEANDERS AND MASUR–VEECH VOLUMES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 23 March 2020, e4
-
- Article
-
- You have access
- Open access
- Export citation
SUMS OF SQUARES AND PARTITION CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 249-267
- Print publication:
- October 2021
-
- Article
- Export citation
Tropical friezes and the index in higher homological algebra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 23-49
- Print publication:
- July 2021
-
- Article
- Export citation
Bootstrapping partition regularity of linear systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 09 March 2020, pp. 630-653
-
- Article
- Export citation
On minimal Ramsey graphs and Ramsey equivalence in multiple colours
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 09 March 2020, pp. 537-554
-
- Article
- Export citation
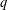 $q$-DEFORMED RATIONALS AND
$q$-DEFORMED RATIONALS AND 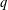 $q$-CONTINUED FRACTIONS
$q$-CONTINUED FRACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
Directed preferential attachment models: Limiting degree distributions and their tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 122-136
- Print publication:
- March 2020
-
- Article
- Export citation
An invariance principle and a large deviation principle for the biased random walk on
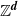 ${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 295-313
- Print publication:
- March 2020
-
- Article
- Export citation
Limit theorems for process-level Betti numbers for sparse and critical regimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 1-31
- Print publication:
- March 2020
-
- Article
- Export citation
The existence of a giant cluster for percolation on large Crump–Mode–Jagers trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 266-290
- Print publication:
- March 2020
-
- Article
- Export citation
A preferential attachment process approaching the Rado graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 27 February 2020, pp. 443-455
-
- Article
- Export citation
Percolation on an infinitely generated group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 587-615
-
- Article
- Export citation
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
POWER PARTITIONS AND SEMI-
 $m$-FIBONACCI PARTITIONS
$m$-FIBONACCI PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 418-429
- Print publication:
- December 2020
-
- Article
- Export citation
Turán numbers of theta graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 495-507
-
- Article
- Export citation
UNIFORM ASYMPTOTIC FORMULAS FOR RESTRICTED BIPARTITE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 217-225
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
On subgraphs of C2k-free graphs and a problem of Kühn and Osthus
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 436-454
-
- Article
- Export citation