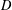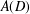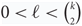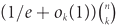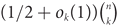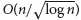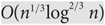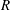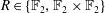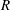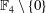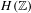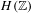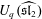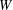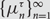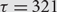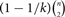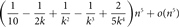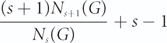Refine listing
Actions for selected content:
1718 results in 05xxx
SINGULARITY OF ORIENTED GRAPHS FROM SEVERAL CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 7-14
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Edge-statistics on large graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 163-189
-
- Article
- Export citation
Monochromatic trees in random tournaments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 November 2019, pp. 318-345
-
- Article
- Export citation
The string of diamonds is nearly tight for rumour spreading
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 190-199
-
- Article
- Export citation
Spectra of Boolean Graphs Over Finite Fields of Characteristic Two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 58-65
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Unlabelled Gibbs partitions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 293-309
-
- Article
- Export citation
Non-triviality of the Poisson boundary of random walks on the group
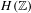 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1160-1189
- Print publication:
- April 2021
-
- Article
- Export citation
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e39
-
- Article
-
- You have access
- Open access
- Export citation
On the Brownian separable permuton
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 24 October 2019, pp. 241-266
-
- Article
- Export citation
A NOTE ON NORMALISED HEAT DIFFUSION FOR GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 1-6
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
DEGREE OF THE
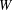 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 186-200
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On the number of symbols that forces a transversal
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 October 2019, pp. 234-240
-
- Article
- Export citation
On Ramsey numbers of hedgehogs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 101-112
-
- Article
- Export citation
The Infinite limit of random permutations avoiding patterns of length three
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 October 2019, pp. 137-152
-
- Article
- Export citation
Minimizing the number of 5-cycles in graphs with given edge-density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 October 2019, pp. 44-67
-
- Article
- Export citation
Extensions of the Erdős–Gallai theorem and Luo’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 128-136
-
- Article
- Export citation
Long Monotone Trails in Random Edge-Labellings of Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 22-30
-
- Article
- Export citation
THE THICKNESS OF SCHUBERT CELLS AS INCIDENCE STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 145-156
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
The Induced Removal Lemma in Sparse Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 153-162
-
- Article
- Export citation
UNIFORM SPANNING FORESTS OF PLANAR GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 September 2019, e29
-
- Article
-
- You have access
- Open access
- Export citation