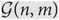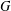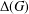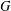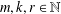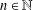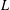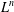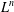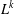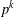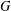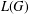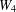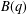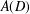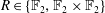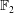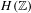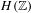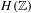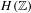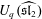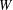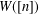Refine listing
Actions for selected content:
1766 results in 05xxx
Counting subgraphs in fftp graphs with symmetry
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 327-353
- Print publication:
- March 2021
-
- Article
- Export citation
Avoiding long Berge cycles: the missing cases k = r + 1 and k = r + 2
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 423-435
-
- Article
- Export citation
Sharp concentration of the equitable chromatic number of dense random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 213-233
-
- Article
- Export citation
CHARACTER GRAPHS WITH NONBIPARTITE HAMILTONIAN COMPLEMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 25 November 2019, pp. 91-95
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Separation dimension and degree
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 549-558
- Print publication:
- May 2021
-
- Article
- Export citation
A RAMSEY TYPE RESULT FOR LATIN SQUARES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 362-366
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON THE CROSSING NUMBER OF THE JOIN OF THE WHEEL ON FIVE VERTICES WITH THE DISCRETE GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 353-361
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF COEFFICIENTS OF THE MOCK THETA FUNCTION
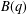 $B(q)$
$B(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 50-58
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
SINGULARITY OF ORIENTED GRAPHS FROM SEVERAL CLASSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 7-14
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Edge-statistics on large graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 163-189
-
- Article
- Export citation
Monochromatic trees in random tournaments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 November 2019, pp. 318-345
-
- Article
- Export citation
The string of diamonds is nearly tight for rumour spreading
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 190-199
-
- Article
- Export citation
Spectra of Boolean Graphs Over Finite Fields of Characteristic Two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 58-65
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Unlabelled Gibbs partitions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 293-309
-
- Article
- Export citation
Non-triviality of the Poisson boundary of random walks on the group
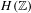 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1160-1189
- Print publication:
- April 2021
-
- Article
- Export citation
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e39
-
- Article
-
- You have access
- Open access
- Export citation
On the Brownian separable permuton
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 24 October 2019, pp. 241-266
-
- Article
- Export citation
A NOTE ON NORMALISED HEAT DIFFUSION FOR GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 1-6
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
DEGREE OF THE
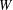 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 186-200
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On the number of symbols that forces a transversal
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 October 2019, pp. 234-240
-
- Article
- Export citation