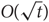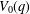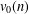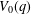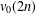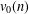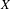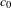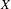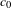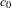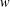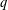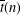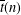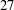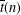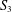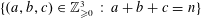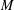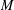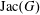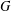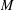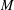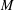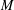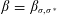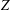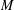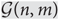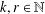Refine listing
Actions for selected content:
1718 results in 05xxx
A note on the Brown–Erdős–Sós conjecture in groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 633-640
-
- Article
- Export citation
On Extensions for Gentle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 249-292
- Print publication:
- February 2021
-
- Article
- Export citation
Two-graphs and the Embedded Topology of Smooth Quartics and its Bitangent Lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 802-812
- Print publication:
- December 2020
-
- Article
- Export citation
OVERPARTITIONS RELATED TO THE MOCK THETA FUNCTION
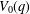 $V_{0}(q)$
$V_{0}(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 410-417
- Print publication:
- December 2020
-
- Article
- Export citation
A NEW COARSELY RIGID CLASS OF BANACH SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 1729-1747
- Print publication:
- September 2021
-
- Article
- Export citation
RANK GENERATING FUNCTIONS FOR ODD-BALANCED UNIMODAL SEQUENCES, QUANTUM JACOBI FORMS, AND MOCK JACOBI FORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 157-175
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
CLOSED FORMS FOR DEGENERATE BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 207-217
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On Baire measurable colorings of group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 818-845
- Print publication:
- March 2021
-
- Article
- Export citation
INFINITE FAMILIES OF CONGRUENCES FOR OVERPARTITIONS WITH RESTRICTED ODD DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 59-66
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A DISTRIBUTION ON TRIPLES WITH MAXIMUM ENTROPY MARGINAL
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 09 December 2019, e46
-
- Article
-
- You have access
- Open access
- Export citation
GEOMETRIC BIJECTIONS FOR REGULAR MATROIDS, ZONOTOPES, AND EHRHART THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 December 2019, e45
-
- Article
-
- You have access
- Open access
- Export citation
The replica symmetric phase of random constraint satisfaction problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 03 December 2019, pp. 346-422
-
- Article
- Export citation
Counting subgraphs in fftp graphs with symmetry
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 327-353
- Print publication:
- March 2021
-
- Article
- Export citation
Avoiding long Berge cycles: the missing cases k = r + 1 and k = r + 2
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 423-435
-
- Article
- Export citation
Sharp concentration of the equitable chromatic number of dense random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 213-233
-
- Article
- Export citation
CHARACTER GRAPHS WITH NONBIPARTITE HAMILTONIAN COMPLEMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 25 November 2019, pp. 91-95
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Separation dimension and degree
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 549-558
- Print publication:
- May 2021
-
- Article
- Export citation
A RAMSEY TYPE RESULT FOR LATIN SQUARES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 362-366
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON THE CROSSING NUMBER OF THE JOIN OF THE WHEEL ON FIVE VERTICES WITH THE DISCRETE GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 353-361
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF COEFFICIENTS OF THE MOCK THETA FUNCTION
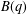 $B(q)$
$B(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 50-58
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation