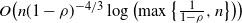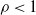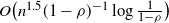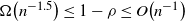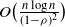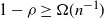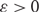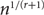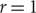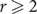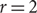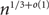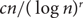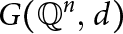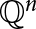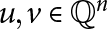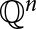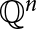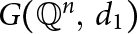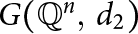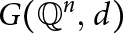Refine listing
Actions for selected content:
1718 results in 05xxx
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
Trees grown under young-age preferential attachment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 911-927
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Improved queue-size scaling for input-queued switches via graph factorization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 798-824
- Print publication:
- September 2020
-
- Article
- Export citation
Flooding and diameter in general weighted random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 956-980
- Print publication:
- September 2020
-
- Article
- Export citation
Dirac’s theorem for random regular graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 17-36
-
- Article
- Export citation
Monochromatic cycle partitions in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 136-152
-
- Article
-
- You have access
- Open access
- Export citation
Many disjoint triangles in co-triangle-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 153-162
-
- Article
- Export citation
Improved Ramsey-type results for comparability graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 13 August 2020, pp. 747-756
-
- Article
- Export citation
Robustness of randomized rumour spreading
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 August 2020, pp. 37-78
-
- Article
-
- You have access
- Open access
- Export citation
Extremal problems for convex geometric hypergraphs and ordered hypergraphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 10 August 2020, pp. 1648-1666
- Print publication:
- December 2021
-
- Article
- Export citation
A quantitative Lovász criterion for Property B
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 07 August 2020, pp. 956-960
-
- Article
- Export citation
Beyond Beatty sequences: Complementary lattices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 06 August 2020, pp. 499-511
- Print publication:
- September 2021
-
- Article
- Export citation
Approximately counting bases of bicircular matroids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 06 August 2020, pp. 124-135
-
- Article
- Export citation
THE COMBINATORICS OF TENSOR PRODUCTS OF HIGHER AUSLANDER ALGEBRAS OF TYPE A
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 526-546
- Print publication:
- September 2021
-
- Article
- Export citation
On Single-Distance Graphs on the Rational Points in Euclidean Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 13-24
- Print publication:
- March 2021
-
- Article
- Export citation
On the subgraph query problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 27 July 2020, pp. 1-16
-
- Article
- Export citation
Mallows permutations as stable matchings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 27 July 2020, pp. 1531-1555
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
Large triangle packings and Tuza’s conjecture in sparse random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 22 July 2020, pp. 757-779
-
- Article
- Export citation
Pseudorandom hypergraph matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 22 July 2020, pp. 868-885
-
- Article
- Export citation
A note on distinct distances
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 650-663
-
- Article
- Export citation