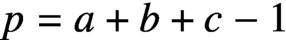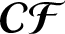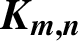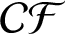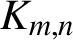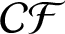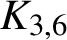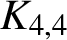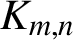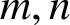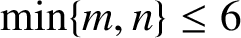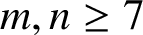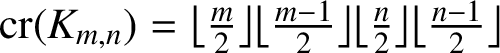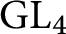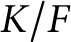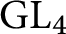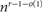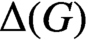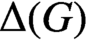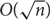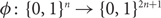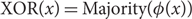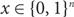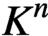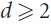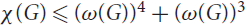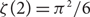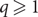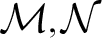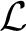Refine listing
Actions for selected content:
1718 results in 05xxx
Dynamics of plane partitions: Proof of the Cameron–Fon-Der-Flaass conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 07 December 2020, 62
-
- Article
-
- You have access
- Open access
- Export citation
THE GENERAL POSITION NUMBER OF THE CARTESIAN PRODUCT OF TWO TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 04 December 2020, pp. 1-10
- Print publication:
- August 2021
-
- Article
- Export citation
Large complete minors in random subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 619-630
-
- Article
- Export citation
ON PROBLEMS OF
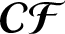 $\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR
$\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR 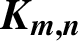 $\boldsymbol{K}_{\boldsymbol{m,n}}$
$\boldsymbol{K}_{\boldsymbol{m,n}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 203-210
- Print publication:
- October 2021
-
- Article
- Export citation
Limit theorems for assortativity and clustering in null models for scale-free networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1035-1084
- Print publication:
- December 2020
-
- Article
- Export citation
A proof of the linear Arithmetic Fundamental Lemma for
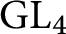 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 381-427
- Print publication:
- April 2022
-
- Article
- Export citation
Generalizations of the Ruzsa–Szemerédi and rainbow Turán problems for cliques
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 19 November 2020, pp. 591-608
-
- Article
-
- You have access
- Open access
- Export citation
THE CHARACTER GRAPH OF A FINITE GROUP IS PERFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 127-131
- Print publication:
- August 2021
-
- Article
- Export citation
Lipschitz bijections between boolean functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 513-525
-
- Article
- Export citation
Making Kr+1-free graphs r-partite
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 10 November 2020, pp. 609-618
-
- Article
-
- You have access
- Open access
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
- Print publication:
- June 2021
-
- Article
- Export citation
MULTINOMIAL VANDERMONDE CONVOLUTION VIA PERMANENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 353-361
- Print publication:
- June 2021
-
- Article
- Export citation
Subgraph counts for dense random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 460-497
-
- Article
- Export citation
Asymptotic normality in t-stack sortable permutations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 04 November 2020, pp. 1062-1070
-
- Article
- Export citation
Disjointness graphs of segments in the space
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 04 November 2020, pp. 498-512
-
- Article
- Export citation
The bandwidth theorem for locally dense graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e42
-
- Article
-
- You have access
- Open access
- Export citation
A rainbow blow-up lemma for almost optimally bounded edge-colourings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 October 2020, e37
-
- Article
-
- You have access
- Open access
- Export citation
A discrepancy version of the Hajnal–Szemerédi theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 444-459
-
- Article
- Export citation
The minimum perfect matching in pseudo-dimension 0 < q < 1
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 374-397
-
- Article
-
- You have access
- Open access
- Export citation
PSEUDO-FINITE SETS, PSEUDO-O-MINIMALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 577-599
- Print publication:
- June 2021
-
- Article
- Export citation