Refine listing
Actions for selected content:
1718 results in 05xxx
ON WEAKLY PERFECT ANNIHILATING-IDEAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 11 May 2021, pp. 362-372
- Print publication:
- December 2021
-
- Article
- Export citation
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 92-100
- Print publication:
- February 2022
-
- Article
- Export citation
Log-concavity and log-convexity of moments of averages of i.i.d. random variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 271-278
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Density theorems for anisotropic point configurations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 1244-1276
- Print publication:
- October 2022
-
- Article
- Export citation
Back stable Schubert calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 883-962
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting matchings via capacity-preserving operators
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation
Additive bases via Fourier analysis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 930-941
-
- Article
- Export citation
A Symmetric Function of Increasing Forests
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 29 April 2021, e35
-
- Article
-
- You have access
- Open access
- Export citation
THE METRIC DIMENSION OF THE ANNIHILATING-IDEAL GRAPH OF A FINITE COMMUTATIVE RING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 27 April 2021, pp. 362-368
- Print publication:
- June 2021
-
- Article
- Export citation
Turán theorems for unavoidable patterns
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 423-442
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
ASKING QUESTIONS TO DETERMINE THE PRODUCT OF CIRCULARLY ARRANGED NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 April 2021, pp. 187-195
- Print publication:
- October 2021
-
- Article
- Export citation
Universal and unavoidable graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 15 April 2021, pp. 942-955
-
- Article
-
- You have access
- Open access
- Export citation
Mass-conserving diffusion-based dynamics on graphs
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 423-471
-
- Article
-
- You have access
- Open access
- Export citation
Ramsey-type numbers involving graphs and hypergraphs with large girth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 722-740
-
- Article
- Export citation
Lee-Yang zeros of the antiferromagnetic Ising model
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2172-2206
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the size-Ramsey number of grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 06 April 2021, pp. 670-685
-
- Article
- Export citation
POWERS OF BINOMIAL EDGE IDEALS WITH QUADRATIC GRÖBNER BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 31 March 2021, pp. 233-255
- Print publication:
- June 2022
-
- Article
- Export citation
Tree limits and limits of random trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 31 March 2021, pp. 849-893
-
- Article
-
- You have access
- Open access
- Export citation
A NEW REFINEMENT OF FINE’S PARTITION THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 353-361
- Print publication:
- December 2021
-
- Article
- Export citation
Powers of paths in tournaments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 23 March 2021, pp. 894-898
-
- Article
- Export citation
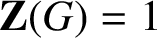
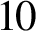
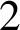
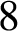
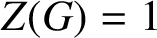
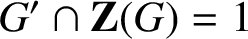
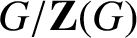
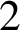
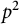
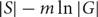
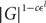
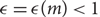
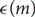
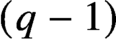
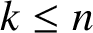
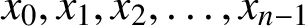
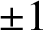
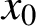
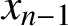
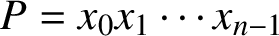
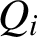
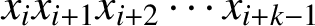
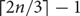 , which is best possible.
, which is best possible.