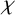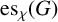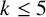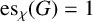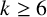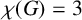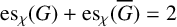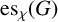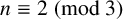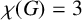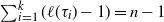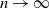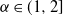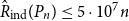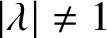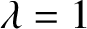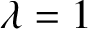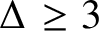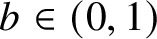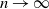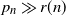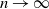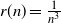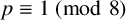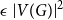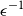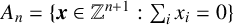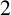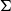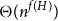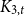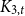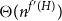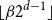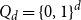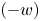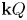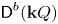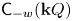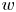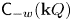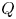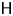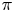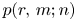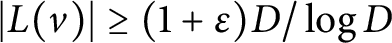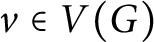Refine listing
Actions for selected content:
1771 results in 05xxx
SOME EXTREMAL RESULTS ON THE CHROMATIC STABILITY INDEX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 185-194
- Print publication:
- October 2022
-
- Article
- Export citation
THEOREMS OF HYPERARITHMETIC ANALYSIS AND ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 31 March 2022, pp. 133-149
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random stable-type minimal factorizations of the n-cycle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 24 February 2022, pp. 1-63
- Print publication:
- March 2022
-
- Article
- Export citation
Packable hyperbolic surfaces with symmetries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 103-113
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Short proofs for long induced paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 870-878
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lee–Yang zeros and the complexity of the ferromagnetic Ising model on bounded-degree graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 07 February 2022, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper Lie automorphisms of incidence algebras
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 07 February 2022, pp. 702-715
-
- Article
- Export citation
Derived categories of skew-gentle algebras and orbifolds
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 649-674
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prevalence of deficiency-zero reaction networks in an Erdös–Rényi framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 384-398
- Print publication:
- June 2022
-
- Article
- Export citation
FINITE TWO-DISTANCE-TRANSITIVE DIHEDRANTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 386-401
-
- Article
- Export citation
Removal lemmas and approximate homomorphisms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 721-736
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABELIAN DIFFERENCE SETS AS LATTICE COVERINGS AND LATTICE TILINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 177-184
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exchangeable and sampling-consistent distributions on rooted binary trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 14 January 2022, pp. 60-80
- Print publication:
- March 2022
-
- Article
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
Subgraph densities in a surface
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 January 2022, pp. 812-839
-
- Article
- Export citation
Independent sets of a given size and structure in the hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 702-720
-
- Article
- Export citation
Functorially finite hearts, simple-minded systems in negative cluster categories, and noncrossing partitions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 23 February 2022, pp. 211-243
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some generating functions and inequalities for the andrews–stanley partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 120-135
-
- Article
- Export citation
Tuning as convex optimisation: a polynomial tuner for multi-parametric combinatorial samplers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 765-811
-
- Article
- Export citation
Independent transversals in bipartite correspondence-covers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 882-894
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation